经典神经网络模块

基本例子

CPU下模型训练

以下的经典神经网络模块均支持自动反向传播计算。当您运行前传函数以后，再执行反向函数就可以计算梯度。一个卷积层的简单例子如下:

from pyvqnet.tensor import arange
from pyvqnet import kfloat32
from pyvqnet.nn import Conv2D

# an image feed into two dimension convolution layer
b = 2        # batch size
ic = 2       # input channels
oc = 2      # output channels
hw = 4      # input width and heights

# two dimension convolution layer
test_conv = Conv2D(ic,oc,(2,2),(2,2),"same")

# input of shape [b,ic,hw,hw]
x0 = arange(1,b*ic*hw*hw+1,requires_grad=True,dtype=kfloat32)

x1 = x0.reshape([b,ic,hw,hw])

#forward function
y = test_conv(x1)

#backward function with autograd
y.backward()
print(x0.grad)
# [-0.0008376 -0.2780731 -0.0008376 -0.2780731  0.1125833  0.2805848
#   0.1125833  0.2805848 -0.0008376 -0.2780731 -0.0008376 -0.2780731
#   0.1125833  0.2805848  0.1125833  0.2805848  0.5759128 -0.057339
#   0.5759128 -0.057339  -0.342508  -0.4853693 -0.342508  -0.4853693
#   0.5759128 -0.057339   0.5759128 -0.057339  -0.342508  -0.4853693
#  -0.342508  -0.4853693 -0.0008376 -0.2780731 -0.0008376 -0.2780731
#   0.1125833  0.2805848  0.1125833  0.2805848 -0.0008376 -0.2780731
#  -0.0008376 -0.2780731  0.1125833  0.2805848  0.1125833  0.2805848
#   0.5759128 -0.057339   0.5759128 -0.057339  -0.342508  -0.4853693
#  -0.342508  -0.4853693  0.5759128 -0.057339   0.5759128 -0.057339
#  -0.342508  -0.4853693 -0.342508  -0.4853693]

GPU下模型训练

您需要安装linux版本下的pyvqnet才能使用GPU。需要保证数据QTensor以及Module均在GPU上。可使用 toGPU 转移数据或者 gpu 创建副本，或者在数据创建函数中使用device指定。

请参考以下例子：

from pyvqnet.tensor import arange
from pyvqnet import kfloat32,DEV_GPU_0
from pyvqnet.nn import Conv2D


b = 2        # batch size
ic = 2       # input channels
oc = 2      # output channels
hw = 4      # input width and heights


test_conv = Conv2D(ic,oc,(2,2),(2,2),"same")
#复制到gpu上DEV_GPU_0
test_conv.toGPU(DEV_GPU_0)
# input of shape [b,ic,hw,hw]
x0 = arange(1,b*ic*hw*hw+1,requires_grad=True,dtype=kfloat32).reshape([b,ic,hw,hw])

#使用gpu 复制数据到DEV_GPU_0，亦可以在函数内指定ID，也可以使用相关tensor接口的device进行指定
x0 = x0.GPU(DEV_GPU_0)
x0.requires_grad = True
#forward function
x = test_conv(x0)

#backward function with autograd
x.backward()
print(x0.grad)

Module类

abstract calculation module

Module

class pyvqnet.nn.module.Module

所有神经网络模块的基类,包括量子模块或经典模块。您的模型也应该是此类的子类,用于 autograd 计算。 模块还可以包含其他Module类,允许将它们嵌套在树状结构。 您可以将子模块分配为常规属性:

class Model(Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = pyvqnet.nn.Conv2d(1, 20, (5,5))
        self.conv2 = pyvqnet.nn.Conv2d(20, 20, (5,5))
    def forward(self, x):
        x = pyvqnet.nn.activation.relu(self.conv1(x))
        return pyvqnet.nn.activation.relu(self.conv2(x))

以这种方式分配的子模块将被注册。

forward

pyvqnet.nn.module.Module.forward(x, *args, **kwargs)

Module类抽象前向计算函数

Parameters:

• x – 输入QTensor。

• *args – 非关键字可变参数。

• **kwargs – 关键字可变参数。

Returns:

模型输出。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
import pyvqnet as vq
from pyvqnet.nn import Conv2D
b = 2
ic = 3
oc = 2
test_conv = Conv2D(ic, oc, (3, 3), (2, 2), "same")
x0 = QTensor(np.arange(1, b * ic * 5 * 5 + 1).reshape([b, ic, 5, 5]),
            requires_grad=True,
            dtype=vq.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[[4.3995643, 3.9317808, -2.0707254],
#  [20.1951981, 21.6946659, 14.2591858],
#  [38.4702759, 31.9730244, 24.5977650]],
# [[-17.0607567, -31.5377998, -7.5618000],
#  [-22.5664024, -40.3876266, -15.1564388],
#  [-3.1080279, -18.5986233, -8.0648050]]],
# [[[6.6493244, -13.4840755, -20.2554188],
#  [54.4235802, 34.4462433, 26.8171902],
#  [90.2827682, 62.9092331, 51.6892929]],
# [[-22.3385429, -45.2448578, 5.7101378],
#  [-32.9464149, -60.9557228, -10.4994345],
#  [5.9029331, -20.5480480, -0.9379558]]]
# ]

state_dict

pyvqnet.nn.module.Module.state_dict(destination=None, prefix='')

返回包含模块整个状态的字典:包括参数和缓存值。 键是对应的参数和缓存值名称。

Parameters:

• destination – 返回保存模型内部模块,参数的字典。

• prefix – 使用的参数和缓存值的命名前缀。

Returns:

包含模块整个状态的字典。

Example:

from pyvqnet.nn import Conv2D
test_conv = Conv2D(2,3,(3,3),(2,2),"same")
print(test_conv.state_dict().keys())
#odict_keys(['weights', 'bias'])

toGPU

pyvqnet.nn.module.Module.toGPU(device: int = DEV_GPU_0)

将模块和其子模块的参数和缓冲数据移动到指定的 GPU 设备中。

device 指定存储其内部数据的设备。 当device >= DEV_GPU_0时，数据存储在GPU上。如果您的计算机有多个GPU， 则可以指定不同的设备来存储数据。例如device = DEV_GPU_1 , DEV_GPU_2, DEV_GPU_3, … 表示存储在不同序列号的GPU上。

Note

Module在不同GPU上无法进行计算。 如果您尝试在 ID 超过验证 GPU 最大数量的 GPU 上创建 QTensor，将引发 Cuda 错误。

Parameters:

device – 当前保存QTensor的设备，默认=DEV_GPU_0。device= pyvqnet.DEV_GPU_0，存储在第一个 GPU 中，devcie = DEV_GPU_1，存储在第二个 GPU 中，依此类推

Returns:

Module 移动到 GPU 设备。

Examples:

from pyvqnet.nn.conv import ConvT2D
test_conv = ConvT2D(3, 2, [4,4], [2, 2], "same")
test_conv = test_conv.toGPU()
print(test_conv.backend)
#1000

toCPU

pyvqnet.nn.module.Module.toCPU()

将模块和其子模块的参数和缓冲数据移动到特定的 CPU 设备中。

Returns:

Module 移动到 CPU 设备。

Examples:

from pyvqnet.nn.conv import ConvT2D
test_conv = ConvT2D(3, 2, [4,4], [2, 2], "same")
test_conv = test_conv.toCPU()
print(test_conv.backend)
#0

模型参数保存和载入

以下接口可以进行模型参数保存到文件中，或从文件中读取参数文件。但请注意，文件中不保存模型结构，需要用户手动构建模型结构。

save_parameters

pyvqnet.utils.storage.save_parameters(obj, f)

保存模型参数的字典到一个文件。

Parameters:

• obj – 需要保存的字典。

• f – 保存参数的文件名。

Returns:

无。

Example:

from pyvqnet.nn import Module,Conv2D
import pyvqnet
class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = Conv2D(input_channels=1, output_channels=6, kernel_size=(5, 5), stride=(1, 1), padding="valid")

    def forward(self, x):
        return super().forward(x)

model = Net()
pyvqnet.utils.storage.save_parameters(model.state_dict(),"tmp.model")

load_parameters

pyvqnet.utils.storage.load_parameters(f)

从文件中载入参数到一个字典中。

Parameters:

f – 保存参数的文件名。

Returns:

保存参数的字典。

Example:

from pyvqnet.nn import Module, Conv2D
import pyvqnet


class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = Conv2D(input_channels=1,
                            output_channels=6,
                            kernel_size=(5, 5),
                            stride=(1, 1),
                            padding="valid")

    def forward(self, x):
        return super().forward(x)

model = Net()
model1 = Net()  # another Module object
pyvqnet.utils.storage.save_parameters(model.state_dict(), "tmp.model")
model_para = pyvqnet.utils.storage.load_parameters("tmp.model")
model1.load_state_dict(model_para)

ModuleList

class pyvqnet.nn.module.ModuleList([pyvqnet.nn.module.Module])

将子模块保存在列表中。 ModuleList 可以像普通的 Python 列表一样被索引， 它包含的Module的内部参数等可以被保存起来。

Parameters:

modules – nn.Modules 列表

Returns:

一个模块列表

Example:

from pyvqnet.tensor import *
from pyvqnet.nn import Module,Linear,ModuleList
from pyvqnet.qnn import ProbsMeasure,QuantumLayer
import pyqpanda as pq
def pqctest (input,param,qubits,cubits,m_machine):
    circuit = pq.QCircuit()
    circuit.insert(pq.H(qubits[0]))
    circuit.insert(pq.H(qubits[1]))
    circuit.insert(pq.H(qubits[2]))
    circuit.insert(pq.H(qubits[3]))

    circuit.insert(pq.RZ(qubits[0],input[0]))
    circuit.insert(pq.RZ(qubits[1],input[1]))
    circuit.insert(pq.RZ(qubits[2],input[2]))
    circuit.insert(pq.RZ(qubits[3],input[3]))

    circuit.insert(pq.CNOT(qubits[0],qubits[1]))
    circuit.insert(pq.RZ(qubits[1],param[0]))
    circuit.insert(pq.CNOT(qubits[0],qubits[1]))

    circuit.insert(pq.CNOT(qubits[1],qubits[2]))
    circuit.insert(pq.RZ(qubits[2],param[1]))
    circuit.insert(pq.CNOT(qubits[1],qubits[2]))

    circuit.insert(pq.CNOT(qubits[2],qubits[3]))
    circuit.insert(pq.RZ(qubits[3],param[2]))
    circuit.insert(pq.CNOT(qubits[2],qubits[3]))
    #print(circuit)

    prog = pq.QProg()
    prog.insert(circuit)

    rlt_prob = ProbsMeasure([0,2],prog,m_machine,qubits)
    return rlt_prob


class M(Module):
    def __init__(self):
        super(M, self).__init__()
        self.pqc2 = ModuleList([QuantumLayer(pqctest,3,"cpu",4,1), Linear(4,1)
        ])

    def forward(self, x, *args, **kwargs):
        y = self.pqc2[0](x)  + self.pqc2[1](x)
        return y

mm = M()
print(mm.state_dict().keys())
#odict_keys(['pqc2.0.m_para', 'pqc2.1.weights', 'pqc2.1.bias'])

ParameterList

class pyvqnet.nn.module.ParameterList([pyvqnet.nn.module.Module])

将参数保存在列表中, ParameterList 可以像普通的 Python 列表一样被索引， 它包含的Parameter的内部参数等可以被保存起来。

Parameters:

modules – nn.Parameter 列表

Returns:

一个参数列表

Example:

from pyvqnet import nn
class MyModule(nn.Module):
    def __init__(self):
        super().__init__()
        self.params = nn.ParameterList([nn.Parameter((10, 10)) for i in range(10)])
    def forward(self, x):

        # ParameterList can act as an iterable, or be indexed using ints
        for i, p in enumerate(self.params):
            x = self.params[i // 2] * x + p * x
        return x

model = MyModule()
print(model.state_dict().keys())

Sequential

class pyvqnet.nn.module.Sequential([pyvqnet.nn.module.Module])

模块将按照传递的顺序添加模块。或者，也可以将模块的 OrderedDict 传入。Sequential 的 forward() 方法接受任何输入，并将其转发给它的第一个模块。 然后将输出依次 “链 “到其后每个模块的输入、最后返回最后一个模块的输出。

Parameters:

modules – 添加的Module

Returns:

Sequential

Example:

from pyvqnet import nn
from collections import OrderedDict

# 使用Sequential创建一个小模型
model = nn.Sequential(
          nn.Conv2D(1,20,(5, 5)),
          nn.ReLu(),
          nn.Conv2D(20,64,(5, 5)),
          nn.ReLu()
        )
print(model.state_dict().keys())

# 基于OrderedDict来使用Sequential, 代码如下

model = nn.Sequential(OrderedDict([
          ('conv1', nn.Conv2D(1,20,(5, 5))),
          ('relu1', nn.ReLu()),
          ('conv2', nn.Conv2D(20,64,(5, 5))),
          ('relu2', nn.ReLu())
        ]))
print(model.state_dict().keys())

经典神经网络层

以下实现了一些经典神经网络层：卷积，转置卷积，池化，归一化，循环神经网络等。

Conv1D

class pyvqnet.nn.Conv1D(input_channels: int, output_channels: int, kernel_size: int, stride: int = 1, padding='valid', use_bias: bool = True, kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, group: int = 1, dtype=None, name='')

在输入上进行一维卷积运算。 Conv1D模块的输入具有形状(batch_size、input_channels、in_height)。

Parameters:

• input_channels – int - 输入数据的通道数。

• output_channels – int - 输出数据的通道数。

• kernel_size – int - 卷积核的尺寸. 卷积核形状 = [output_channels,input_channels/group,kernel_size,1]。

• stride – int - 步长, 默认为1。

• padding – str|int - 填充选项, 它可以是一个字符串 {‘valid’, ‘same’} 或一个整数，给出应用在输入上的填充量。 默认 “valid”。

• use_bias – bool - 是否使用偏置项, 默认使用。

• kernel_initializer – callable - 卷积核初始化方法。默认为空,使用kaiming_uniform。

• bias_initializer – callable - 偏置初始化方法。默认为空,使用kaiming_uniform。

• dilation_rate – int - 空洞大小,defaults: 1。

• group – int - 分组卷积的分组数. Default: 1。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 模块的名字,default:””。

Returns:

一维卷积实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的out_height 为 = ceil(in_height / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Conv1D
import pyvqnet
b= 2
ic =3
oc = 2
test_conv = Conv1D(ic,oc,3,2,"same")
x0 = QTensor(np.arange(1,b*ic*5*5 +1).reshape([b,ic,25]),requires_grad=True,dtype=pyvqnet.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[12.4438553, 14.8618164, 15.5595102, 16.2572021, 16.9548950, 17.6525879, 18.3502808, 19.0479736, 19.7456665, 20.4433594, 21.1410522, 21.8387432, 10.5725441],
#  [-13.7539215, 1.0263026, 1.2747254, 1.5231485, 1.7715728, 2.0199962, 2.2684195, 2.5168428, 2.7652662, 3.0136888, 3.2621140, 3.5105357, 14.0515862]],
# [[47.4924164, 41.0252953, 41.7229881, 42.4206772, 43.1183739, 43.8160667, 44.5137596, 45.2114487, 45.9091415, 46.6068344, 47.3045311, 48.0022240, 18.3216572],
#  [-47.2381554, 10.3421783, 10.5906038, 10.8390274, 11.0874519, 11.3358765, 11.5842953, 11.8327246, 12.0811434, 12.3295631, 12.5779924, 12.8264122, 39.4719162]]
# ]

Conv2D

class pyvqnet.nn.Conv2D(input_channels: int, output_channels: int, kernel_size: tuple, stride: tuple = (1, 1), padding='valid', use_bias=True, kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, group: int = 1, dtype=None, name='')

在输入上进行二维卷积运算。 Conv2D模块的输入具有形状(batch_size, input_channels, height, width)。

Parameters:

• input_channels – int - 输入数据的通道数。

• output_channels – int - 输出数据的通道数。

• kernel_size – tuple|list - 卷积核的尺寸. 卷积核形状 = [output_channels,input_channels/group,kernel_size,kernel_size]。

• stride – tuple|list - 步长, 默认为 (1, 1)|[1,1]。

• padding – str|tuple - 填充选项, 它可以是一个字符串 {‘valid’, ‘same’} 或一个整数元组，给出在两边应用的隐式填充量。 默认 “valid”。

• use_bias – bool - 是否使用偏置项, 默认使用。

• kernel_initializer – callable - 卷积核初始化方法。默认为空,使用kaiming_uniform。

• bias_initializer – callable - 偏置初始化方法。默认为空,使用kaiming_uniform。

• dilation_rate – int - 空洞大小,defaults: 1。

• group – int - 分组卷积的分组数. Default: 1。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 模块的名字,default:””。

Returns:

二维卷积实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的height 为 = ceil(height / stride), 输出的width 为 = ceil(width / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Conv2D
import pyvqnet
b= 2
ic =3
oc = 2
test_conv = Conv2D(ic,oc,(3,3),(2,2),"same")
x0 = QTensor(np.arange(1,b*ic*5*5+1).reshape([b,ic,5,5]),requires_grad=True,dtype=pyvqnet.kfloat32)
x = test_conv.forward(x0)
print(x)

# [
# [[[-0.1256833, 23.8978596, 26.7449780],
#  [-7.2959919, 33.4023743, 42.1283913],
#  [-8.7684336, 25.2698975, 40.4024887]],
# [[33.0653763, 40.3120155, 27.3781891],
#  [39.2921371, 45.8685760, 38.1885109],
#  [23.1873779, 12.0480318, 12.7278290]]],
# [[[-0.9730744, 61.3967094, 79.0511856],
#  [-29.3652401, 75.0349350, 112.7325439],
#  [-26.4682808, 59.0924797, 104.2572098]],
# [[66.8064194, 96.0953140, 72.9157486],
#  [90.9154129, 110.7232437, 91.2616043],
#  [56.8825951, 34.6904907, 30.1957760]]]
# ]

ConvT2D

class pyvqnet.nn.ConvT2D(input_channels, output_channels, kernel_size, stride=[1, 1], padding='valid', use_bias='True', kernel_initializer=None, bias_initializer=None, dilation_rate: int = 1, group: int = 1, dtype=None, name='')

在输入上进行二维转置卷积运算。 Conv2D模块的输入具有形状(batch_size, input_channels, height, width)。

Parameters:

• input_channels – int - 输入数据的通道数。

• output_channels – int - 输出数据的通道数。

• kernel_size – tuple|list - 卷积核的尺寸,卷积核形状 = [input_channels,output_channels/group,kernel_size,kernel_size]。

• stride – tuple|list - 步长, 默认为 (1, 1)|[1,1]。

• padding – str|tuple - 填充选项, 它可以是一个字符串 {‘valid’, ‘same’} 或一个整数元组，给出在两边应用的隐式填充量。 默认 “valid”。

• use_bias – bool - 是否使用偏置项, 默认使用。

• kernel_initializer – callable - 卷积核初始化方法。默认为空,使用kaiming_uniform。

• bias_initializer – callable - 偏置项初始化方法。默认为空,使用kaiming_uniform。

• dilation_rate – int - 空洞大小,defaults: 1。

• group – int - 分组卷积的分组数. Default: 1。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 模块的名字,default:””。

Returns:

二维转置卷积实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的height 为 = ceil(height / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import ConvT2D
import pyvqnet
test_conv = ConvT2D(3, 2, (3, 3), (1, 1), "valid")
x = QTensor(np.arange(1, 1 * 3 * 5 * 5+1).reshape([1, 3, 5, 5]), requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-3.3675897, 4.8476148, 14.2448473, 14.8897810, 15.5347166, 20.0420666, 10.9831696],
#  [-14.0110836, -3.2500827, 6.4022207, 6.5149083, 6.6275964, 23.7946320, 12.1828709],
#  [-22.2661152, -3.5112300, 12.9493723, 13.5486069, 14.1478367, 39.6327629, 18.8349991],
#  [-24.4063797, -3.0093837, 15.9455290, 16.5447617, 17.1439915, 44.7691879, 21.3293095],
#  [-26.5466480, -2.5075383, 18.9416828, 19.5409145, 20.1401463, 49.9056053, 23.8236179],
#  [-24.7624626, -13.7395811, -7.9510674, -7.9967723, -8.0424776, 19.2783546, 7.0562835],
#  [-3.5170188, 10.2280807, 16.1939259, 16.6804695, 17.1670132, 21.2262039, 6.2889833]],
# [[-2.0570512, -9.5056667, -25.0429192, -25.9464111, -26.8499031, -24.7305946, -16.9881954],
#  [-0.7620960, -18.3383904, -49.8948288, -51.2528229, -52.6108208, -52.2179604, -34.3664169],
#  [-11.7121849, -27.1864738, -62.2154846, -63.6433640, -65.0712280, -52.6787071, -38.4497032],
#  [-13.3643141, -29.0211792, -69.3548126, -70.7826691, -72.2105408, -58.1659012, -43.7543182],
#  [-15.0164423, -30.8558884, -76.4941254, -77.9219971, -79.3498535, -63.6530838, -49.0589256],
#  [-11.6070204, -14.1940546, -35.5471687, -36.0715408, -36.5959129, -23.9147663, -22.8668022],
#  [-14.4390459, -4.9011412, -6.4719801, -6.5418491, -6.6117167, 9.3329525, -1.7254852]]]
# ]

AvgPool1D

class pyvqnet.nn.AvgPool1D(kernel, stride, padding='valid', name='')

对一维输入进行平均池化。输入具有形状(batch_size, input_channels, in_height)。

Parameters:

• kernel – 平均池化的窗口大小。

• strides – 窗口移动的步长。

• padding – 填充选项, “valid” or “same” 或者整数指定填充长度。 默认 “valid”。

• name – 模块的名字,default:””。

Returns:

一维平均池化层实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的out_height 为 = ceil(in_height / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import AvgPool1D
test_mp = AvgPool1D([3],[2],"same")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
# [
# [[0.3333333, 1.6666666, 3.],
#  [1.6666666, 2., 1.3333334],
#  [2.6666667, 2.6666667, 2.3333333],
#  [2.3333333, 4.3333335, 3.3333333],
#  [0.3333333, 1.6666666, 4.]]
# ]

MaxPool1D

class pyvqnet.nn.MaxPool1D(kernel, stride, padding='valid', name='')

对一维输入进行最大池化。输入具有形状(batch_size, input_channels, in_height)。

Parameters:

• kernel – 最大池化的窗口大小。

• strides – 窗口移动的步长。

• padding – 填充选项, “valid” or “same” 或者整数指定填充长度。 默认 “valid”。

• name – 命名,默认为””。

Returns:

一维最大池化层实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的out_height 为 = ceil(in_height / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import MaxPool1D
test_mp = MaxPool1D([3],[2],"same")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
#[[[1. 4. 5.]
#   [3. 3. 3.]
#   [4. 4. 4.]
#   [5. 6. 6.]
#   [1. 5. 7.]]]

AvgPool2D

class pyvqnet.nn.AvgPool2D(kernel, stride, padding='valid', name='')

对二维输入进行平均池化。输入具有形状(batch_size, input_channels, height, width)。

Parameters:

• kernel – 平均池化的窗口大小。

• strides – 窗口移动的步长。

• padding – 填充选项, “valid” or “same” 或包含2个整数的元组，整数为两个维度上的填充长度。 默认 “valid”。

• name – 命名,默认为””。

Returns:

二维平均池化层实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的height 为 = ceil(height / stride), 输出的width 为 = ceil(width / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import AvgPool2D
test_mp = AvgPool2D([2,2],[2,2],"valid")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
#[[[[1.5  1.75]
#    [3.75 3.  ]]]]

MaxPool2D

class pyvqnet.nn.MaxPool2D(kernel, stride, padding='valid', name='')

对二维输入进行最大池化。输入具有形状(batch_size, input_channels, height, width)。

Parameters:

• kernel – 最大池化的窗口大小。

• strides – 窗口移动的步长。

• padding – 填充选项, “valid” or “same” 或包含2个整数的元组，整数为两个维度上的填充长度。 默认 “valid”。

• name – 命名,默认为””。

Returns:

二维最大池化层实例。

Note

padding='valid' 不进行填充。

padding='same' 补零填充输入,输出的height 为 = ceil(height / stride), 输出的width 为 = ceil(width / stride)。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import MaxPool2D
test_mp = MaxPool2D([2,2],[2,2],"valid")
x= QTensor(np.array([0, 1, 0, 4, 5,
                            2, 3, 2, 1, 3,
                            4, 4, 0, 4, 3,
                            2, 5, 2, 6, 4,
                            1, 0, 0, 5, 7],dtype=float).reshape([1,1,5,5]),requires_grad=True)

y= test_mp.forward(x)
print(y)
# [[[[3. 4.]
#    [5. 6.]]]]

Embedding

class pyvqnet.nn.embedding.Embedding(num_embeddings, embedding_dim, weight_initializer=xavier_normal, dtype=None, name: str = '')

该模块通常用于存储词嵌入并使用索引检索它们。模块的输入是索引列表,输出是对应的词嵌入。 该层的输入应该是kint64。

Parameters:

• num_embeddings – int - 嵌入字典的大小。

• embedding_dim – int - 每个嵌入向量的大小

• weight_initializer – callable - 参数初始化方式,默认正态分布。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 嵌入层的命名,默认为””。

Returns:

a Embedding 实例。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn.embedding import Embedding
import pyvqnet
vlayer = Embedding(30,3)
x = QTensor(np.arange(1,25).reshape([2,3,2,2]),dtype= pyvqnet.kint64)
y = vlayer(x)
print(y)

# [
# [[[[-0.3168081, 0.0329394, -0.2934906],
#  [0.1057295, -0.2844988, -0.1687456]],
# [[-0.2382513, -0.3642318, -0.2257225],
#  [0.1563180, 0.1567665, 0.3038477]]],
# [[[-0.4131152, -0.0564500, -0.2804018],
#  [-0.2955172, -0.0009581, -0.1641144]],
# [[0.0692555, 0.1094901, 0.4099118],
#  [0.4348361, 0.0304361, -0.0061203]]],
# [[[-0.3310401, -0.1836129, 0.1098949],
#  [-0.1840732, 0.0332474, -0.0261806]],
# [[-0.1489778, 0.2519453, 0.3299376],
#  [-0.1942692, -0.1540277, -0.2335350]]]],
# [[[[-0.2620637, -0.3181309, -0.1857461],
#  [-0.0878164, -0.4180320, -0.1831555]],
# [[-0.0738970, -0.1888980, -0.3034399],
#  [0.1955448, -0.0409723, 0.3023460]]],
# [[[0.2430045, 0.0880465, 0.4309453],
#  [-0.1796514, -0.1432367, -0.1253638]],
# [[-0.5266719, 0.2386262, -0.0329155],
#  [0.1033449, -0.3442690, -0.0471130]]],
# [[[-0.5336705, -0.1939755, -0.3000667],
#  [0.0059001, 0.5567381, 0.1926173]],
# [[-0.2385869, -0.3910453, 0.2521235],
#  [-0.0246447, -0.0241158, -0.1402829]]]]
# ]

BatchNorm2d

class pyvqnet.nn.BatchNorm2d(channel_num: int, momentum: float = 0.1, epsilon: float = 1e-05, beta_initializer=zeros, gamma_initializer=ones, dtype=None, name='')

在 4D 输入(B、C、H、W)上应用批归一化。参照论文 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 。

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

其中 \(\gamma\) 和 \(\beta\) 为待训练参数。此外,默认情况下,在训练期间,该层会继续运行估计其计算的均值和方差,然后在评估期间用于归一化。平均方差均值保持默认动量 0.1。

Parameters:

• channel_num – int - 输入通道数。

• momentum – float - 计算指数加权平均时的动量,默认为 0.1。

• beta_initializer – callable - beta的初始化方式,默认全零初始化。

• gamma_initializer – callable - gamma的的初始化方式,默认全一初始化。

• epsilon – float - 数值稳定参数, 默认 1e-5。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 批归一化层命名,默认为””。

Returns:

二维批归一化层实例。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import BatchNorm2d
import pyvqnet
b = 2
ic = 2
test_conv = BatchNorm2d(ic)

x = QTensor(np.arange(1, 17).reshape([b, ic, 4, 1]),
            requires_grad=True,
            dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-1.3242440],
#  [-1.0834724],
#  [-0.8427007],
#  [-0.6019291]],
# [[-1.3242440],
#  [-1.0834724],
#  [-0.8427007],
#  [-0.6019291]]],
# [[[0.6019291],
#  [0.8427007],
#  [1.0834724],
#  [1.3242440]],
# [[0.6019291],
#  [0.8427007],
#  [1.0834724],
#  [1.3242440]]]
# ]

BatchNorm1d

class pyvqnet.nn.BatchNorm1d(channel_num: int, momentum: float = 0.1, epsilon: float = 1e-05, beta_initializer=zeros, gamma_initializer=ones, dtype=None, name='')

在 2D 输入 (B,C) 上进行批归一化操作。 参照论文 Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift 。

\[y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

其中 \(\gamma\) 和 \(\beta\) 为待训练参数。此外,默认情况下,在训练期间,该层会继续运行估计其计算的均值和方差,然后在评估期间用于归一化。平均方差均值保持默认动量 0.1。

Parameters:

• channel_num – int - 输入通道数。

• momentum – float - 计算指数加权平均时的动量,默认为 0.1。

• beta_initializer – callable - beta的初始化方式,默认全零初始化。

• gamma_initializer – callable - gamma的的初始化方式,默认全一初始化。

• epsilon – float - 数值稳定性常数,默认为 1e-5。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 批归一化层命名,默认为””。

Returns:

一维批归一化层实例。

Example:

import numpy as np
from pyvqnet.tensor import QTensor
from pyvqnet.nn import BatchNorm1d
import pyvqnet
test_conv = BatchNorm1d(4)

x = QTensor(np.arange(1, 17).reshape([4, 4]),
            requires_grad=True,
            dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [-1.3416405, -1.3416405, -1.3416405, -1.3416405],
# [-0.4472135, -0.4472135, -0.4472135, -0.4472135],
# [0.4472135, 0.4472135, 0.4472135, 0.4472135],
# [1.3416405, 1.3416405, 1.3416405, 1.3416405]
# ]

LayerNormNd

class pyvqnet.nn.layer_norm.LayerNormNd(normalized_shape: list, epsilon: float = 1e-05, affine: bool = True, dtype=None, name='')

在任意输入的后D个维度上进行层归一化。具体方式如论文所述: Layer Normalization。

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

对于像 (B,C,H,W,D) 这样的输入， norm_shape 可以是 [C,H,W,D],[H,W,D],[W,D] 或 [D] .

Parameters:

• norm_shape – float - 标准化形状。

• epsilon – float - 数值稳定性常数，默认为 1e-5。

• affine – bool - 是否使用应用仿射变换，默认为 True。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

一个 LayerNormNd 类

Example:

import numpy as np
from pyvqnet.tensor import QTensor,kfloat32
from pyvqnet.nn.layer_norm import LayerNormNd
ic = 4
test_conv = LayerNormNd([2,2])
x = QTensor(np.arange(1,17).reshape([2,2,2,2]),requires_grad=True,dtype=kfloat32)
y = test_conv.forward(x)
print(y)
# [
# [[[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]],
# [[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]]],
# [[[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]],
# [[-1.3416355, -0.4472118],
#  [0.4472118, 1.3416355]]]
# ]

LayerNorm2d

class pyvqnet.nn.layer_norm.LayerNorm2d(norm_size: int, epsilon: float = 1e-05, affine: bool = True, dtype=None, name='')

在 4D 输入上进行层归一化。具体方式如论文所述: Layer Normalization。

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

平均值和标准差是在除去第一个维度以外的剩余维度数据上计算的。对于像 (B,C,H,W) 这样的输入, norm_size 应该等于 C * H * W。

Parameters:

• norm_size – float - 归一化大小,应该等于 C * H * W。

• epsilon – float - 数值稳定性常数,默认为 1e-5。

• affine – bool - 是否使用应用仿射变换，默认为 True。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

二维层归一化实例。

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn.layer_norm import LayerNorm2d
ic = 4
test_conv = LayerNorm2d(8)
x = QTensor(np.arange(1,17).reshape([2,2,4,1]),requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [[[-1.5275238],
#  [-1.0910884],
#  [-0.6546531],
#  [-0.2182177]],
# [[0.2182177],
#  [0.6546531],
#  [1.0910884],
#  [1.5275238]]],
# [[[-1.5275238],
#  [-1.0910884],
#  [-0.6546531],
#  [-0.2182177]],
# [[0.2182177],
#  [0.6546531],
#  [1.0910884],
#  [1.5275238]]]
# ]

LayerNorm1d

class pyvqnet.nn.layer_norm.LayerNorm1d(norm_size: int, epsilon: float = 1e-05, affine: bool = True, dtype=None, name='')

在 2D 输入上进行层归一化。具体方式如论文所述: Layer Normalization。

\[y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta\]

均值和标准差是在最后一个维度大小上计算的,其中“norm_size” 是 norm_size 的值。

Parameters:

• norm_size – float - 归一化大小,应该等于最后一维大小。

• epsilon – float - 数值稳定性常数,默认为 1e-5。

• affine – bool - 是否使用应用仿射变换，默认为 True。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

一维层归一化实例。

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn.layer_norm import LayerNorm1d
test_conv = LayerNorm1d(4)
x = QTensor(np.arange(1,17).reshape([4,4]),requires_grad=True,dtype=pyvqnet.kfloat32)
y = test_conv.forward(x)
print(y)

# [
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355],
# [-1.3416355, -0.4472118, 0.4472118, 1.3416355]
# ]

Linear

class pyvqnet.nn.Linear(input_channels, output_channels, weight_initializer=None, bias_initializer=None, use_bias=True, dtype=None, name: str = '')

线性模块(全连接层)。 \(y = Ax + b\)

Parameters:

• input_channels – int - 输入数据通道数。

• output_channels – int - 输出数据通道数。

• weight_initializer – callable - 权重初始化函数,默认为空,使用he_uniform。

• bias_initializer – callable - 偏置初始化参数,默认为空,使用he_uniform。

• use_bias – bool - 是否使用偏置项, 默认使用。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 线性层的命名,默认为””。

Returns:

线性层实例。

Example:

import numpy as np
import pyvqnet
from pyvqnet.tensor import QTensor
from pyvqnet.nn import Linear
c1 =2
c2 = 3
cin = 7
cout = 5
n = Linear(cin,cout)
input = QTensor(np.arange(1,c1*c2*cin+1).reshape((c1,c2,cin)),requires_grad=True,dtype=pyvqnet.kfloat32)
y = n.forward(input)
print(y)

# [
# [[4.3084583, -1.9228780, -0.3428757, 1.2840536, -0.5865945],
#  [9.8339605, -5.5135884, -3.1228657, 4.3025794, -4.1492314],
#  [15.3594627, -9.1042995, -5.9028554, 7.3211040, -7.7118683]],
# [[20.8849659, -12.6950111, -8.6828451, 10.3396301, -11.2745066],
#  [26.4104652, -16.2857227, -11.4628344, 13.3581581, -14.8371439],
#  [31.9359703, -19.8764324, -14.2428246, 16.3766804, -18.3997803]]
# ]

Dropout

class pyvqnet.nn.dropout.Dropout(dropout_rate=0.5)

Dropout 模块。dropout 模块将一些单元的输出随机设置为零,同时根据给定的 dropout_rate 概率升级其他单元。

Parameters:

• dropout_rate – float - 神经元被设置为零的概率。

• name – 这个模块的名字， 默认为””。

Returns:

Dropout实例。

Example:

import numpy as np
from pyvqnet.nn.dropout import Dropout
from pyvqnet.tensor import QTensor
b = 2
ic = 2
x = QTensor(np.arange(-1 * ic * 2 * 2,
                    (b - 1) * ic * 2 * 2).reshape([b, ic, 2, 2]),
            requires_grad=True)
droplayer = Dropout(0.5)
droplayer.train()
y = droplayer(x)
print(y)

# [
# [[[-16., -14.],
#  [-0., -0.]],
# [[-8., -6.],
#  [-4., -2.]]],
# [[[0., 2.],
#  [4., 6.]],
# [[8., 10.],
#  [0., 14.]]]
# ]

Pixel_Shuffle

class pyvqnet.nn.pixel_shuffle.Pixel_Shuffle(upscale_factors, name='')

重新排列形状为：(, C * r^2, H, W) 的张量 到形状为 (, C, H * r, W * r) 的张量，其中 r 是尺度变换因子。

Parameters:

• upscale_factors – 增加尺度变换的因子

• name – 这个模块的名字， 默认为””。

Returns:

Pixel_Shuffle 模块

Example:

from pyvqnet.nn import Pixel_Shuffle
from pyvqnet.tensor import tensor
ps = Pixel_Shuffle(3)
inx = tensor.ones([5,2,3,18,4,4])
inx.requires_grad=  True
y = ps(inx)
print(y.shape)
#[5, 2, 3, 2, 12, 12]

Pixel_Unshuffle

class pyvqnet.nn.pixel_shuffle.Pixel_Unshuffle(downscale_factors, name='')

通过重新排列元素来反转 Pixel_Shuffle 操作. 将 (, C, H * r, W * r) 形状的张量变化为 (, C * r^2, H, W) ，其中 r 是缩小因子。

Parameters:

• downscale_factors – 增加尺度变换的因子

• name – 这个模块的名字， 默认为””。

Returns:

Pixel_Unshuffle 模块

Example:

from pyvqnet.nn import Pixel_Unshuffle
from pyvqnet.tensor import tensor
ps = Pixel_Unshuffle(3)
inx = tensor.ones([5, 2, 3, 2, 12, 12])
inx.requires_grad = True
y = ps(inx)
print(y.shape)
#[5, 2, 3, 18, 4, 4]

GRU

class pyvqnet.nn.gru.GRU(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

门控循环单元 (GRU) 模块。支持多层堆叠，双向配置。单层单向GRU的计算公式如下:

\[\begin{split}\begin{array}{ll} r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)} \end{array}\end{split}\]

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏特征维度。

• num_layers – 堆叠GRU层数， 默认: 1。

• batch_first – 如果为 True， 则输入形状为 [batch_size,seq_len,feature_dim]， 如果为 False， 则输入形状为 [seq_len,batch_size,feature_dim]，默认为 True。

• use_bias – 如果为 False，该模块不适用偏置项，默认: True。

• bidirectional – 如果为 True, 变为双向GRU， 默认: False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

GRU 实例

Example:

from pyvqnet.nn import GRU
from pyvqnet.tensor import tensor

rnn2 = GRU(4, 6, 2, batch_first=False, bidirectional=True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])

output, hn = rnn2(input, h0)
print(output)
print(hn)
# [
# [[0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [0.2815045, 0.2056844, 0.0750246, 0.5802019, 0.3536537, 0.8136684, -0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812]],
# [[0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840],
#  [0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840],
#  [0.0490867, 0.0115325, -0.2797680, 0.4711050, -0.0687061, 0.7216146, 0.0258964, 0.0619203, 0.6341010, 0.8445141, -0.4164453, 0.7409840]],
# [[0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123],
#  [0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123],
#  [0.0182974, -0.0536071, -0.4478674, 0.4315647, -0.2191887, 0.6492687, 0.1572548, 0.0839213, 0.6707115, 0.8444533, -0.3811499, 0.7448123]],
# [[0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759],
#  [0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759],
#  [0.0722285, -0.0636698, -0.5457084, 0.3817562, -0.1890205, 0.5696942, 0.3855782, 0.2057217, 0.7370453, 0.8646453, -0.1967214, 0.7630759]],
# [[0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535, 0.6941375, 0.4570828, 0.8433002, 0.9152645, 0.2342478, 0.8299093]]
# ]
# [
# [[-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725],
#  [-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725],
#  [-0.8070476, -0.5560303, 0.7575479, -0.2368367, 0.4228620, -0.2573725]],
# [[-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730],
#  [-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730],
#  [-0.3857390, -0.3195596, 0.0281313, 0.8734715, -0.4499536, 0.2270730]],
# [[0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535],
#  [0.1834545, -0.0489200, -0.6343678, 0.3061281, -0.0449328, 0.4901535]],
# [[-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812],
#  [-0.0034523, 0.1634004, 0.6099871, 0.8451654, -0.2833570, 0.7294812]]
# ]

RNN

class pyvqnet.nn.rnn.RNN(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

循环神经网络(RNN)模块，使用 \(\tanh\) 或 \(\text{ReLU}\) 作为激活函数。支持双向，多层配置。 单层单向RNN计算公式如下:

\[h_t = \tanh(W_{ih} x_t + b_{ih} + W_{hh} h_{(t-1)} + b_{hh})\]

如果 nonlinearity 是 'relu', 则 \(\text{ReLU}\) 将替代 \(\tanh\)。

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏特征维度。

• num_layers – 堆叠RNN层数， 默认: 1。

• nonlinearity – 非线性激活函数，默认为 'tanh'。

• batch_first – 如果为 True， 则输入形状为 [batch_size,seq_len,feature_dim]， 如果为 False， 则输入形状为 [seq_len,batch_size,feature_dim]，默认为 True。

• use_bias – 如果为 False， 该模块不适用偏置项，默认: True。

• bidirectional – 如果为 True，变为双向RNN，默认: False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

RNN 实例

Example:

from pyvqnet.nn import RNN
from pyvqnet.tensor import tensor

rnn2 = RNN(4, 6, 2, batch_first=False, bidirectional = True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])
output, hn = rnn2(input, h0)
print(output)
print(hn)

# [[[-0.413501  -0.4584284 -0.7530673  0.017902   0.5038776  0.6589128
#    -0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]
#   [-0.413501  -0.4584284 -0.7530673  0.017902   0.5038776  0.6589128
#    -0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]
#   [-0.413501  -0.4584284 -0.7530673  0.017902   0.5038776  0.6589128
#    -0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]]

#  [[ 0.2127696 -0.6644132 -0.3884572 -0.0344413  0.35414    0.5639224
#    -0.2358238  0.7706838 -0.3650029 -0.54729   -0.2392456 -0.3285939]
#   [ 0.2127696 -0.6644132 -0.3884572 -0.0344413  0.35414    0.5639224
#    -0.2358238  0.7706838 -0.3650029 -0.54729   -0.2392456 -0.3285939]
#   [ 0.2127696 -0.6644132 -0.3884572 -0.0344413  0.35414    0.5639224
#    -0.2358238  0.7706838 -0.3650029 -0.54729   -0.2392456 -0.3285939]]

#  [[ 0.0432173 -0.3811357 -0.4611054 -0.255436   0.4998702  0.6649145
#    -0.3132874  0.5965794 -0.5760088 -0.5618317 -0.2404964 -0.4669401]
#   [ 0.0432173 -0.3811357 -0.4611054 -0.255436   0.4998702  0.6649145
#    -0.3132874  0.5965794 -0.5760088 -0.5618317 -0.2404964 -0.4669401]
#   [ 0.0432173 -0.3811357 -0.4611054 -0.255436   0.4998702  0.6649145
#    -0.3132874  0.5965794 -0.5760088 -0.5618317 -0.2404964 -0.4669401]]

#  [[ 0.1083845 -0.4397578 -0.4745184 -0.2148822  0.3674186  0.6907974
#    -0.061549   0.452508  -0.5262724 -0.3184315 -0.4691838 -0.0438465]
#   [ 0.1083845 -0.4397578 -0.4745184 -0.2148822  0.3674186  0.6907974
#    -0.061549   0.452508  -0.5262724 -0.3184315 -0.4691838 -0.0438465]
#   [ 0.1083845 -0.4397578 -0.4745184 -0.2148822  0.3674186  0.6907974
#    -0.061549   0.452508  -0.5262724 -0.3184315 -0.4691838 -0.0438465]]

#  [[-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067
#    -0.8672301  0.0971878 -0.7561615 -0.5063094  0.5117968 -0.0985391]
#   [-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067
#    -0.8672301  0.0971878 -0.7561615 -0.5063094  0.5117968 -0.0985391]
#   [-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067
#    -0.8672301  0.0971878 -0.7561615 -0.5063094  0.5117968 -0.0985391]]]
# [[[ 0.2451548  0.9127097 -0.6998036  0.6434992  0.1046313  0.6530996]
#   [ 0.2451548  0.9127097 -0.6998036  0.6434992  0.1046313  0.6530996]
#   [ 0.2451548  0.9127097 -0.6998036  0.6434992  0.1046313  0.6530996]]

#  [[-0.1760802 -0.546555   0.7547818  0.8418489 -0.2011115  0.1687339]
#   [-0.1760802 -0.546555   0.7547818  0.8418489 -0.2011115  0.1687339]
#   [-0.1760802 -0.546555   0.7547818  0.8418489 -0.2011115  0.1687339]]

#  [[-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067]
#   [-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067]
#   [-0.1835401 -0.6232781 -0.3571274  0.2283377  0.5426646  0.6719067]]

#  [[-0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]
#   [-0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]
#   [-0.3040171  0.6689512 -0.5059364 -0.4492912 -0.1206206 -0.3208488]]]

LSTM

class pyvqnet.nn.lstm.LSTM(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

长短期记忆(LSTM)模块。支持双向LSTM， 堆叠多层LSTM等配置。单层单向LSTM计算公式如下:

\[\begin{split}\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \\ h_t = o_t \odot \tanh(c_t) \\ \end{array}\end{split}\]

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏特征维度。

• num_layers – 堆叠LSTM层数，默认: 1。

• batch_first – 如果为 True，则输入形状为 [batch_size,seq_len,feature_dim]， 如果为 False, 则输入形状为 [seq_len,batch_size,feature_dim]，默认为 True。

• use_bias – 如果为 False，该模块不适用偏置项， 默认: True。

• bidirectional – 如果为 True，变为双向LSTM， 默认: False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

LSTM 实例

Example:

from pyvqnet.nn import LSTM
from pyvqnet.tensor import tensor

rnn2 = LSTM(4, 6, 2, batch_first=False, bidirectional = True)

input = tensor.ones([5, 3, 4])
h0 = tensor.ones([4, 3, 6])
c0 = tensor.ones([4, 3, 6])
output, (hn, cn) = rnn2(input, (h0, c0))

print(output)
print(hn)
print(cn)

# [[[ 0.2732482  0.1701475  0.1449948  0.0736707  0.1340735  0.1299259
#     0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]
#   [ 0.2732482  0.1701475  0.1449948  0.0736707  0.1340735  0.1299259
#     0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]
#   [ 0.2732482  0.1701475  0.1449948  0.0736707  0.1340735  0.1299259
#     0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]]

#  [[ 0.0973835  0.2728153  0.0826659  0.1486651  0.001023  -0.0002572
#     0.0662036  0.2953667  0.0374205  0.1520839 -0.1803852 -0.0302957]
#   [ 0.0973835  0.2728153  0.0826659  0.1486651  0.001023  -0.0002572
#     0.0662036  0.2953667  0.0374205  0.1520839 -0.1803852 -0.0302957]
#   [ 0.0973835  0.2728153  0.0826659  0.1486651  0.001023  -0.0002572
#     0.0662036  0.2953667  0.0374205  0.1520839 -0.1803852 -0.0302957]]

#  [[ 0.0228571  0.1898227  0.0312898  0.1559544 -0.0909701 -0.0543313
#     0.0921322  0.3542943  0.0323457  0.1877485 -0.1509136  0.0398105]
#   [ 0.0228571  0.1898227  0.0312898  0.1559544 -0.0909701 -0.0543313
#     0.0921322  0.3542943  0.0323457  0.1877485 -0.1509136  0.0398105]
#   [ 0.0228571  0.1898227  0.0312898  0.1559544 -0.0909701 -0.0543313
#     0.0921322  0.3542943  0.0323457  0.1877485 -0.1509136  0.0398105]]

#  [[-0.0164866  0.1411722 -0.002618   0.1457977 -0.1280925 -0.0702658
#     0.1419625  0.4266106  0.0363048  0.2426503 -0.0849762  0.1489675]
#   [-0.0164866  0.1411722 -0.002618   0.1457977 -0.1280925 -0.0702658
#     0.1419625  0.4266106  0.0363048  0.2426503 -0.0849762  0.1489675]
#   [-0.0164866  0.1411722 -0.002618   0.1457977 -0.1280925 -0.0702658
#     0.1419625  0.4266106  0.0363048  0.2426503 -0.0849762  0.1489675]]

#  [[-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742
#     0.2645994  0.4319879  0.0528811  0.3815826  0.1058483  0.1233259]
#   [-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742
#     0.2645994  0.4319879  0.0528811  0.3815826  0.1058483  0.1233259]
#   [-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742
#     0.2645994  0.4319879  0.0528811  0.3815826  0.1058483  0.1233259]]]
# [[[ 0.1752738 -0.0356635  0.2989266  0.20517   -0.0896036  0.5098922]
#   [ 0.1752738 -0.0356635  0.2989266  0.20517   -0.0896036  0.5098922]
#   [ 0.1752738 -0.0356635  0.2989266  0.20517   -0.0896036  0.5098922]]

#  [[-0.2443907 -0.0827548 -0.1557958  0.1731217 -0.0342197 -0.1101249]
#   [-0.2443907 -0.0827548 -0.1557958  0.1731217 -0.0342197 -0.1101249]
#   [-0.2443907 -0.0827548 -0.1557958  0.1731217 -0.0342197 -0.1101249]]

#  [[-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742]
#   [-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742]
#   [-0.0223669  0.1591602 -0.0311901  0.0958475 -0.122227  -0.0682742]]

#  [[ 0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]
#   [ 0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]
#   [ 0.0551452  0.2563322  0.040974   0.1358014 -0.1953781 -0.061493 ]]]
# [[[ 0.3543518 -0.1842273  0.8745036  0.6013567 -0.1227313  1.0065726]
#   [ 0.3543518 -0.1842273  0.8745036  0.6013567 -0.1227313  1.0065726]
#   [ 0.3543518 -0.1842273  0.8745036  0.6013567 -0.1227313  1.0065726]]

#  [[-0.5912023 -0.2058601 -0.4632604  0.3671726 -0.0673411 -0.327456 ]
#   [-0.5912023 -0.2058601 -0.4632604  0.3671726 -0.0673411 -0.327456 ]
#   [-0.5912023 -0.2058601 -0.4632604  0.3671726 -0.0673411 -0.327456 ]]

#  [[-0.0393696  0.301177  -0.0757513  0.196299  -0.3163165 -0.1804099]
#   [-0.0393696  0.301177  -0.0757513  0.196299  -0.3163165 -0.1804099]
#   [-0.0393696  0.301177  -0.0757513  0.196299  -0.3163165 -0.1804099]]

#  [[ 0.1547394  0.4916601  0.1061193  0.2582704 -0.3499697 -0.1048216]
#   [ 0.1547394  0.4916601  0.1061193  0.2582704 -0.3499697 -0.1048216]
#   [ 0.1547394  0.4916601  0.1061193  0.2582704 -0.3499697 -0.1048216]]]

Dynamic_GRU

class pyvqnet.nn.gru.Dynamic_GRU(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

将多层门控循环单元 (GRU) RNN 应用于动态长度输入序列。

第一个输入应该是定义了可变长度的批处理序列输入 通过 tensor.PackedSequence 类。 tensor.PackedSequence 类可以构造为 连续调用下一个函数: pad_sequence 、 pack_pad_sequence。

Dynamic_GRU 的第一个输出也是一个 tensor.PackedSequence 类， 可以使用 tensor.pad_pack_sequence 将其解压缩为普通 QTensor。

对于输入序列中的每个元素，每一层计算以下公式：

\[\begin{split}\begin{array}{ll} r_t = \sigma(W_{ir} x_t + b_{ir} + W_{hr} h_{(t-1)} + b_{hr}) \\ z_t = \sigma(W_{iz} x_t + b_{iz} + W_{hz} h_{(t-1)} + b_{hz}) \\ n_t = \tanh(W_{in} x_t + b_{in} + r_t * (W_{hn} h_{(t-1)}+ b_{hn})) \\ h_t = (1 - z_t) * n_t + z_t * h_{(t-1)} \end{array}\end{split}\]

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏的特征维度。

• num_layers – 循环层数。 默认值：1

• batch_first – 如果为 True，输入形状提供为 [批大小,序列长度,特征维度]。如果为 False，输入形状提供为 [序列长度,批大小,特征维度]，默认为 True。

• use_bias – 如果为False，则该层不使用偏置权重b_ih和b_hh。 默认值：True。

• bidirectional – 如果为真，则成为双向 GRU。 默认值：False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

一个 Dynamic_GRU 类

Example:

from pyvqnet.nn import Dynamic_GRU
from pyvqnet.tensor import tensor
seq_len = [4,1,2]
input_size = 4
batch_size =3
hidden_size = 2
ml = 2
rnn2 = Dynamic_GRU(input_size,
                hidden_size=2,
                num_layers=2,
                batch_first=False,
                bidirectional=True)

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])

y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, hn = rnn2(input, h0)

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)
print(seq_unpacked)
print(lens_unpacked)
# [
# [[-0.3918380, 0.0056273, 0.9018179, 0.9006662],
#  [-0.3715909, 0.0307644, 0.9756137, 0.9705784],
#  [-0.3917399, 0.0057521, 0.9507942, 0.9456232]],
# [[-0.6348240, -0.0603764, 0.9014163, 0.8903066],
#  [0., 0., 0., 0.],
#  [-0.6333261, -0.0592172, 0.9660671, 0.9580816]],
# [[-0.4571511, 0.0210018, 0.9151242, 0.9011748],
#  [0., 0., 0., 0.],
#  [0., 0., 0., 0.]],
# [[-0.3585358, 0.0918219, 0.9496037, 0.9391552],
#  [0., 0., 0., 0.],
#  [0., 0., 0., 0.]]
# ]
# [4 1 2]

Dynamic_RNN

class pyvqnet.nn.rnn.Dynamic_RNN(input_size, hidden_size, num_layers=1, nonlinearity='tanh', batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

将循环神经网络 RNN 应用于动态长度输入序列。

第一个输入应该是定义了可变长度的批处理序列输入 通过 tensor.PackedSequence 类。 tensor.PackedSequence 类可以构造为 连续调用下一个函数: pad_sequence 、 pack_pad_sequence。

Dynamic_RNN 的第一个输出也是一个 tensor.PackedSequence 类， 可以使用 tensor.pad_pack_sequence 将其解压缩为普通 QTensor。

循环神经网络(RNN)模块，使用 \(\tanh\) 或 \(\text{ReLU}\) 作为激活函数。支持双向，多层配置。 单层单向RNN计算公式如下:

\[h_t = \tanh(W_{ih} x_t + b_{ih} + W_{hh} h_{(t-1)} + b_{hh})\]

如果 nonlinearity 是 'relu', 则 \(\text{ReLU}\) 将替代 \(\tanh\)。

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏特征维度。

• num_layers – 堆叠RNN层数， 默认: 1。

• nonlinearity – 非线性激活函数，默认为 'tanh'。

• batch_first – 如果为 True， 则输入形状为 [批大小,序列长度,特征维度]， 如果为 False， 则输入形状为 [序列长度,批大小,特征维度]，默认为 True。

• use_bias – 如果为 False， 该模块不适用偏置项，默认: True。

• bidirectional – 如果为 True，变为双向RNN，默认: False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

Dynamic_RNN 实例

Example:

from pyvqnet.nn import Dynamic_RNN
from pyvqnet.tensor import tensor
seq_len = [4,1,2]
input_size = 4
batch_size =3
hidden_size = 2
ml = 2
rnn2 = Dynamic_RNN(input_size,
                hidden_size=2,
                num_layers=2,
                batch_first=False,
                bidirectional=True,
                nonlinearity='relu')

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])

y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, hn = rnn2(input, h0)

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)
print(seq_unpacked)
print(lens_unpacked)

# [
# [[1.2980951, 0., 0., 0.],
#  [1.5040692, 0., 0., 0.],
#  [1.4927036, 0., 0., 0.1065927]],
# [[2.6561704, 0., 0., 0.2532321],
#  [0., 0., 0., 0.],
#  [3.1472805, 0., 0., 0.]],
# [[5.1231661, 0., 0., 0.7596353],
#  [0., 0., 0., 0.],
#  [0., 0., 0., 0.]],
# [[8.4954977, 0., 0., 0.8191229],
#  [0., 0., 0., 0.],
#  [0., 0., 0., 0.]]
# ]
# [4 1 2]

Dynamic_LSTM

class pyvqnet.nn.lstm.Dynamic_LSTM(input_size, hidden_size, num_layers=1, batch_first=True, use_bias=True, bidirectional=False, dtype=None, name: str = '')

将长短期记忆(LSTM) RNN 应用于动态长度输入序列。

第一个输入应该是定义了可变长度的批处理序列输入 通过 tensor.PackedSequence 类。 tensor.PackedSequence 类可以构造为 连续调用下一个函数: pad_sequence 、 pack_pad_sequence。

Dynamic_LSTM 的第一个输出也是一个 tensor.PackedSequence 类， 可以使用 tensor.pad_pack_sequence 将其解压缩为普通 QTensor。

循环神经网络(RNN)模块，使用 \(\tanh\) 或 \(\text{ReLU}\) 作为激活函数。支持双向，多层配置。 单层单向RNN计算公式如下:

\[\begin{split}\begin{array}{ll} \\ i_t = \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t = \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t = \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t = \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \\ h_t = o_t \odot \tanh(c_t) \\ \end{array}\end{split}\]

Parameters:

• input_size – 输入特征维度。

• hidden_size – 隐藏特征维度。

• num_layers – 堆叠LSTM层数，默认: 1。

• batch_first – 如果为 True，则输入形状为 [批大小,序列长度,特征维度]， 如果为 False, 则输入形状为 [序列长度,批大小,特征维度]，默认为 True。

• use_bias – 如果为 False，该模块不适用偏置项， 默认: True。

• bidirectional – 如果为 True，变为双向LSTM， 默认: False。

• dtype – 参数的数据类型，defaults：None，使用默认数据类型:kfloat32,代表32位浮点数。

• name – 这个模块的名字， 默认为””。

Returns:

Dynamic_LSTM 实例

Example:

from pyvqnet.nn import Dynamic_LSTM
from pyvqnet.tensor import tensor

input_size = 2
hidden_size = 2
ml = 2
seq_len = [3, 4, 1]
batch_size = 3
rnn2 = Dynamic_LSTM(input_size,
                    hidden_size=hidden_size,
                    num_layers=ml,
                    batch_first=False,
                    bidirectional=True)

a = tensor.arange(1, seq_len[0] * input_size + 1).reshape(
    [seq_len[0], input_size])
b = tensor.arange(1, seq_len[1] * input_size + 1).reshape(
    [seq_len[1], input_size])
c = tensor.arange(1, seq_len[2] * input_size + 1).reshape(
    [seq_len[2], input_size])
a.requires_grad = True
b.requires_grad = True
c.requires_grad = True
y = tensor.pad_sequence([a, b, c], False)

input = tensor.pack_pad_sequence(y,
                                seq_len,
                                batch_first=False,
                                enforce_sorted=False)

h0 = tensor.ones([ml * 2, batch_size, hidden_size])
c0 = tensor.ones([ml * 2, batch_size, hidden_size])

output, (hn, cn) = rnn2(input, (h0, c0))

seq_unpacked, lens_unpacked = \
tensor.pad_packed_sequence(output, batch_first=False)

print(seq_unpacked)
print(lens_unpacked)

# [
# [[0.2038177, 0.1139005, 0.2312966, -0.1140076],
#  [0.1992285, 0.1221137, 0.2277344, -0.3147154],
#  [0.2293468, 0.0681745, 0.2426863, 0.2572871]],
# [[0.1398094, -0.0150359, 0.2513067, 0.0783743],
#  [0.1328388, -0.0031956, 0.2324090, -0.1962151],
#  [0., 0., 0., 0.]],
# [[0.0898260, -0.0706460, 0.2396922, 0.2323916],
#  [0.0817787, -0.0449937, 0.2388873, -0.0000469],
#  [0., 0., 0., 0.]],
# [[0., 0., 0., 0.],
#  [0.0532839, -0.0870574, 0.2397324, 0.2103822],
#  [0., 0., 0., 0.]]
# ]
# [3 4 1]

损失函数层

以下为神经网络常用的损失层。

Note

请注意，跟pytorch等框架不同的是，以下loss函数的前向函数中，第一个参数为标签，第二个参数为预测值。

MeanSquaredError

class pyvqnet.nn.MeanSquaredError(name='')

计算输入 \(x\) 和目标值 \(y\) 之间的均方根误差。

若平方根误差可由如下函数描述:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = \left( x_n - y_n \right)^2,\]

\(x\) 和 \(y\) 是任意形状的 QTensor , 总 \(n\) 个元素的均方根误差由下式计算。

\[\ell(x, y) = \operatorname{mean}(L)\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

一个均方根误差实例。

均方根误差前向计算函数的所需参数:

x: \((N, *)\) 预测值,其中 \(*\) 表示任意维度。

y: \((N, *)\), 目标值, 和输入一样维度的 QTensor 。

Note

请注意，跟pytorch等框架不同的是，以下MeanSquaredError函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor, kfloat64
from pyvqnet.nn import MeanSquaredError
y = QTensor([[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]],
            requires_grad=False,
            dtype=kfloat64)
x = QTensor([[0.1, 0.05, 0.7, 0, 0.05, 0.1, 0, 0, 0, 0]],
            requires_grad=True,
            dtype=kfloat64)

loss_result = MeanSquaredError()
result = loss_result(y, x)
print(result)
# [0.0115000]

BinaryCrossEntropy

class pyvqnet.nn.BinaryCrossEntropy(name='')

测量目标和输入之间的平均二元交叉熵损失。

未做平均运算的二元交叉熵如下式:

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_n \left[ y_n \cdot \log x_n + (1 - y_n) \cdot \log (1 - x_n) \right],\]

若 \(N\) 为批的大小,则平均二元交叉熵.

\[\ell(x, y) = \operatorname{mean}(L)\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

一个平均二元交叉熵实例。

平均二元交叉熵误差前向计算函数的所需参数:

x: \((N, *)\) 预测值,其中 \(*\) 表示任意维度。

y: \((N, *)\), 目标值,和输入一样维度的 QTensor 。

Note

请注意，跟pytorch等框架不同的是，BinaryCrossEntropy函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor
from pyvqnet.nn import BinaryCrossEntropy
x = QTensor([[0.3, 0.7, 0.2], [0.2, 0.3, 0.1]], requires_grad=True)
y = QTensor([[0.0, 1.0, 0], [0.0, 0, 1]], requires_grad=False)

loss_result = BinaryCrossEntropy()
result = loss_result(y, x)
result.backward()
print(result)
# [0.6364825]

CategoricalCrossEntropy

class pyvqnet.nn.CategoricalCrossEntropy(name='')

该损失函数将 LogSoftmax 和 NLLLoss 同时计算的平均分类交叉熵。

损失函数计算方式如下,其中 class 为目标值的对应分类标签:

\[\text{loss}(x, y) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

平均分类交叉熵实例。

误差前向计算函数的所需参数:

x: \((N, *)\) 预测值,其中 \(*\) 表示任意维度。

y: \((N, *)\), 目标值,和输入一样维度的 QTensor 。必须为64位整数,kint64。

Note

请注意，跟pytorch等框架不同的是，CategoricalCrossEntropy函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor,kfloat32,kint64
from pyvqnet.nn import CategoricalCrossEntropy
x = QTensor([[1, 2, 3, 4, 5],
[1, 2, 3, 4, 5],
[1, 2, 3, 4, 5]], requires_grad=True,dtype=kfloat32)
y = QTensor([[0, 1, 0, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 0, 0]], requires_grad=False,dtype=kint64)
loss_result = CategoricalCrossEntropy()
result = loss_result(y, x)
print(result)
# [3.7852428]

SoftmaxCrossEntropy

class pyvqnet.nn.SoftmaxCrossEntropy(name='')

该损失函数将 LogSoftmax 和 NLLLoss 同时计算的平均分类交叉熵,并具有更高的数值稳定性。

损失函数计算方式如下,其中 class 为目标值的对应分类标签:

\[\text{loss}(x, y) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

一个Softmax交叉熵损失函数实例

误差前向计算函数的所需参数:

x: \((N, *)\) 预测值,其中 \(*\) 表示任意维度。

y: \((N, *)\), 目标值,和输入一样维度的 QTensor 。必须为64位整数,kint64。

Note

请注意，跟pytorch等框架不同的是，SoftmaxCrossEntropy函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor, kfloat32, kint64
from pyvqnet.nn import SoftmaxCrossEntropy
x = QTensor([[1, 2, 3, 4, 5], [1, 2, 3, 4, 5], [1, 2, 3, 4, 5]],
            requires_grad=True,
            dtype=kfloat32)
y = QTensor([[0, 1, 0, 0, 0], [0, 1, 0, 0, 0], [1, 0, 0, 0, 0]],
            requires_grad=False,
            dtype=kint64)
loss_result = SoftmaxCrossEntropy()
result = loss_result(y, x)
result.backward()
print(result)

# [3.7852478]

NLL_Loss

class pyvqnet.nn.NLL_Loss(name='')

平均负对数似然损失。 对C个类别的分类问题很有用。

x 是模型给出的概率形式的似然量。其尺寸可以是 \((N, C)\) or \((N, C, d_1, d_2, ..., d_K)\) 。 y 是损失函数期望的真值，包含 \([0, C-1]\) 的类别索引。

\[\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - \sum_{n=1}^N \frac{1}{N}x_{n,y_n} \quad\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

一个NLL_Loss损失函数实例

误差前向计算函数的所需参数:

x: \((N, *)\),损失函数的输出预测值，可以为多维变量。

y: \((N, *)\),损失函数目标值。必须为64位整数,kint64。

Note

请注意，跟pytorch等框架不同的是，NLL_Loss函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor, kint64
from pyvqnet.nn import NLL_Loss

x = QTensor([
    0.9476322568516703, 0.226547421131723, 0.5944201443911326,
    0.42830868492969476, 0.76414068655387, 0.00286059168094277,
    0.3574236812873617, 0.9096948856639084, 0.4560809854582528,
    0.9818027091583286, 0.8673569904602182, 0.9860275114020933,
    0.9232667066664217, 0.303693313961628, 0.8461034903175555
])
x.reshape_([1, 3, 1, 5])
x.requires_grad = True
y = QTensor([[[2, 1, 0, 0, 2]]], dtype=kint64)

loss_result = NLL_Loss()
result = loss_result(y, x)
print(result)
#[-0.6187226]

CrossEntropyLoss

class pyvqnet.nn.CrossEntropyLoss(name='')

该函数计算LogSoftmax以及NLL_Loss在一起的损失。

x 是包含未做归一化的输出.它的尺寸可以为 \((C)\) , \((N, C)\) 二维或 \((N, C, d_1, d_2, ..., d_K)\) 多维。

损失函数的公式如下,其中 class 为目标值的对应分类标签:

\[\text{loss}(x, y) = -\log\left(\frac{\exp(x[class])}{\sum_j \exp(x[j])}\right) = -x[class] + \log\left(\sum_j \exp(x[j])\right)\]

Parameters:

name – 这个模块的名字， 默认为””。

Returns:

一个CrossEntropyLoss损失函数实例

误差前向计算函数的所需参数:

x: \((N, *)\),损失函数的输出，可以为多维变量。

y: \((N, *)\),损失函数期望的真值。必须为64位整数,kint64。

Note

请注意，跟pytorch等框架不同的是，CrossEntropyLoss函数的前向函数中，第一个参数为目标值，第二个参数为预测值。

Example:

from pyvqnet.tensor import QTensor, kint64
from pyvqnet.nn import CrossEntropyLoss
x = QTensor([
    0.9476322568516703, 0.226547421131723, 0.5944201443911326,
    0.42830868492969476, 0.76414068655387, 0.00286059168094277,
    0.3574236812873617, 0.9096948856639084, 0.4560809854582528,
    0.9818027091583286, 0.8673569904602182, 0.9860275114020933,
    0.9232667066664217, 0.303693313961628, 0.8461034903175555
])
x.reshape_([1, 3, 1, 5])
x.requires_grad = True
y = QTensor([[[2, 1, 0, 0, 2]]], dtype=kint64)

loss_result = CrossEntropyLoss()
result = loss_result(y, x)
print(result)

#[1.1508200]

激活函数

Activation

class pyvqnet.nn.activation.Activation

激活的基类。 特定的激活函数继承了这个类。

Sigmoid

class pyvqnet.nn.Sigmoid(name: str = '')

Sigmoid激活函数层。

\[\text{Sigmoid}(x) = \frac{1}{1 + \exp(-x)}\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

一个Sigmoid激活函数层实例。

Examples:

from pyvqnet.nn import Sigmoid
from pyvqnet.tensor import QTensor
layer = Sigmoid()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.7310586, 0.8807970, 0.9525741, 0.9820138]

Softplus

class pyvqnet.nn.Softplus(name: str = '')

Softplus激活函数层。

\[\text{Softplus}(x) = \log(1 + \exp(x))\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

一个Softplus激活函数层实例。

Examples:

from pyvqnet.nn import Softplus
from pyvqnet.tensor import QTensor
layer = Softplus()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [1.3132616, 2.1269281, 3.0485873, 4.0181499]

Softsign

class pyvqnet.nn.Softsign(name: str = '')

Softsign 激活函数层。

\[\text{SoftSign}(x) = \frac{x}{ 1 + |x|}\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

一个Softsign 激活函数层实例。

Examples:

from pyvqnet.nn import Softsign
from pyvqnet.tensor import QTensor
layer = Softsign()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.5000000, 0.6666667, 0.7500000, 0.8000000]

Softmax

class pyvqnet.nn.Softmax(axis: int = -1, name: str = '')

Softmax 激活函数层。

\[\text{Softmax}(x_{i}) = \frac{\exp(x_i)}{\sum_j \exp(x_j)}\]

Parameters:

• axis – 计算的维度(最后一个轴为-1),默认值 = -1。

• name – 激活函数层的命名,默认为””。

Returns:

一个Softmax 激活函数层实例。

Examples:

from pyvqnet.nn import Softmax
from pyvqnet.tensor import QTensor
layer = Softmax()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.0320586, 0.0871443, 0.2368828, 0.6439142]

HardSigmoid

class pyvqnet.nn.HardSigmoid(name: str = '')

HardSigmoid 激活函数层。

\[\begin{split}\text{Hardsigmoid}(x) = \begin{cases} 0 & \text{ if } x \le -3, \\ 1 & \text{ if } x \ge +3, \\ x / 6 + 1 / 2 & \text{otherwise} \end{cases}\end{split}\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

一个HardSigmoid 激活函数层实例。

Examples:

from pyvqnet.nn import HardSigmoid
from pyvqnet.tensor import QTensor
layer = HardSigmoid()
y = layer(QTensor([1.0, 2.0, 3.0, 4.0]))
print(y)

# [0.6666667, 0.8333334, 1., 1.]

ReLu

class pyvqnet.nn.ReLu(name: str = '')

ReLu 整流线性单元激活函数层。

\[\begin{split}\text{ReLu}(x) = \begin{cases} x, & \text{ if } x > 0\\ 0, & \text{ if } x \leq 0 \end{cases}\end{split}\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

一个ReLu 激活函数层实例。

Examples:

from pyvqnet.nn import ReLu
from pyvqnet.tensor import QTensor
layer = ReLu()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [0., 2., 0., 4.]

LeakyReLu

class pyvqnet.nn.LeakyReLu(alpha: float = 0.01, name: str = '')

LeakyReLu 带泄露的修正线性单元激活函数层。

\[\begin{split}\text{LeakyRelu}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ \alpha * x, & \text{ otherwise } \end{cases}\end{split}\]

Parameters:

• alpha – LeakyRelu 系数,默认:0.01。

• name – 激活函数层的命名,默认为””。

Returns:

一个LeakyReLu 激活函数层实例。

Examples:

from pyvqnet.nn import LeakyReLu
from pyvqnet.tensor import QTensor
layer = LeakyReLu()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.0100000, 2., -0.0300000, 4.]

ELU

class pyvqnet.nn.ELU(alpha: float = 1, name: str = '')

ELU 指数线性单位激活函数层。

\[\begin{split}\text{ELU}(x) = \begin{cases} x, & \text{ if } x > 0\\ \alpha * (\exp(x) - 1), & \text{ if } x \leq 0 \end{cases}\end{split}\]

Parameters:

• alpha – ELU 系数,默认:1。

• name – 激活函数层的命名,默认为””。

Returns:

ELU 激活函数层实例。

Examples:

from pyvqnet.nn import ELU
from pyvqnet.tensor import QTensor
layer = ELU()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.6321205, 2., -0.9502130, 4.]

Tanh

class pyvqnet.nn.Tanh(name: str = '')

Tanh双曲正切激活函数.

\[\text{Tanh}(x) = \frac{\exp(x) - \exp(-x)} {\exp(x) + \exp(-x)}\]

Parameters:

name – 激活函数层的命名,默认为””。

Returns:

Tanh 激活函数层实例。

Examples:

from pyvqnet.nn import Tanh
from pyvqnet.tensor import QTensor
layer = Tanh()
y = layer(QTensor([-1, 2.0, -3, 4.0]))
print(y)

# [-0.7615942, 0.9640276, -0.9950548, 0.9993293]

优化器模块

Optimizer

class pyvqnet.optim.optimizer.Optimizer(params, lr=0.01)

所有优化器的基类。

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率,默认值:0.01。

Adadelta

class pyvqnet.optim.adadelta.Adadelta(params, lr=0.01, beta=0.99, epsilon=1e-08)

ADADELTA: An Adaptive Learning Rate Method。

参考:https://arxiv.org/abs/1212.5701。

\[\begin{split}E(g_t^2) &= \beta * E(g_{t-1}^2) + (1-\beta) * g^2\\ Square\_avg &= \sqrt{ ( E(dx_{t-1}^2) + \epsilon ) / ( E(g_t^2) + \epsilon ) }\\ E(dx_t^2) &= \beta * E(dx_{t-1}^2) + (1-\beta) * (-g*square\_avg)^2 \\ param\_new &= param - lr * Square\_avg\end{split}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• beta – 用于计算平方梯度的运行平均值(默认值:0.99)。

• epsilon – 添加到分母以提高数值稳定性的常数(默认值:1e-8)。

Returns:

一个 Adadelta 优化器。

Example:

import numpy as np
from pyvqnet.optim import adadelta
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1, 2, 3, 4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1, 2, 3, 4).astype(np.float64))
params = [param]
opti = adadelta.Adadelta(params)

for i in range(1, 3):
    opti._step()
    print(param)

# [
# [[[0., 0.9999900, 1.9999900, 2.9999900],
#  [3.9999900, 4.9999900, 5.9999900, 6.9999900],
#  [7.9999900, 8.9999905, 9.9999905, 10.9999905]],
# [[11.9999905, 12.9999905, 13.9999905, 14.9999905],
#  [15.9999905, 16.9999905, 17.9999905, 18.9999905],
#  [19.9999905, 20.9999905, 21.9999905, 22.9999905]]]
# ]

# [
# [[[0., 0.9999800, 1.9999800, 2.9999800],
#  [3.9999800, 4.9999800, 5.9999800, 6.9999800],
#  [7.9999800, 8.9999800, 9.9999800, 10.9999800]],
# [[11.9999800, 12.9999800, 13.9999800, 14.9999800],
#  [15.9999800, 16.9999809, 17.9999809, 18.9999809],
#  [19.9999809, 20.9999809, 21.9999809, 22.9999809]]]
# ]

Adagrad

class pyvqnet.optim.adagrad.Adagrad(params, lr=0.01, epsilon=1e-08)

Adagrad自适应梯度优化器。

参考:https://databricks.com/glossary/adagrad。

\[\begin{split}\begin{align} moment\_new &= moment + g * g\\param\_new &= param - \frac{lr * g}{\sqrt{moment\_new} + \epsilon} \end{align}\end{split}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• epsilon – 添加到分母以提高数值稳定性的常数(默认值:1e-8)。

Returns:

一个 Adagrad 优化器。

Example:

import numpy as np
from pyvqnet.optim import adagrad
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = adagrad.Adagrad(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0., 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0., 0.9829289, 1.9829290, 2.9829290],
#  [3.9829290, 4.9829288, 5.9829288, 6.9829288],
#  [7.9829288, 8.9829283, 9.9829283, 10.9829283]],
# [[11.9829283, 12.9829283, 13.9829283, 14.9829283],
#  [15.9829283, 16.9829292, 17.9829292, 18.9829292],
#  [19.9829292, 20.9829292, 21.9829292, 22.9829292]]]
# ]

Adam

class pyvqnet.optim.adam.Adam(params, lr=0.01, beta1=0.9, beta2=0.999, epsilon=1e-08, amsgrad: bool = False)

Adam优化器,它可以使用一阶矩估计动态调整每个参数的学习率和梯度的二阶矩估计。

参考:https://arxiv.org/abs/1412.6980。

\[t = t + 1\]

\[moment\_1\_new=\beta1∗moment\_1+(1−\beta1)g\]

\[moment\_2\_new=\beta2∗moment\_2+(1−\beta2)g*g\]

\[lr = lr*\frac{\sqrt{1-\beta2^t}}{1-\beta1^t}\]

如果参数 amsgrad 为 True

\[moment\_2\_max = max(moment\_2\_max,moment\_2)\]

\[param\_new=param-lr*\frac{moment\_1}{\sqrt{moment\_2\_max}+\epsilon}\]

否则

\[param\_new=param-lr*\frac{moment\_1}{\sqrt{moment\_2}+\epsilon}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• beta1 – 用于计算梯度及其平方的运行平均值的系数(默认值:0.9)。

• beta2 – 用于计算梯度及其平方的运行平均值的系数(默认值:0.999)。

• epsilon – 添加到分母以提高数值稳定性的常数(默认值:1e-8)。

• amsgrad – 是否使用该算法的 AMSGrad 变体(默认值:False)。

Returns:

一个 Adam 优化器。

Example:

import numpy as np
from pyvqnet.optim import adam
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = adam.Adam(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0., 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0., 0.9800000, 1.9800000, 2.9800000],
#  [3.9800000, 4.9799995, 5.9799995, 6.9799995],
#  [7.9799995, 8.9799995, 9.9799995, 10.9799995]],
# [[11.9799995, 12.9799995, 13.9799995, 14.9799995],
#  [15.9799995, 16.9799995, 17.9799995, 18.9799995],
#  [19.9799995, 20.9799995, 21.9799995, 22.9799995]]]
# ]

Adamax

class pyvqnet.optim.adamax.Adamax(params, lr=0.01, beta1=0.9, beta2=0.999, epsilon=1e-08)

实现 Adamax 优化器(基于无穷范数的 Adam 变体)。

参考:https://arxiv.org/abs/1412.6980。

\[\begin{split}\\t = t + 1\end{split}\]

\[moment\_new=\beta1∗moment+(1−\beta1)g\]

\[norm\_new = \max{(\beta1∗norm+\epsilon, \left|g\right|)}\]

\[lr = \frac{lr}{1-\beta1^t}\]

\[\begin{split}param\_new = param − lr*\frac{moment\_new}{norm\_new}\\\end{split}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• beta1 – 用于计算梯度及其平方的运行平均值的系数(默认值:0.9)。

• beta2 – 用于计算梯度及其平方的运行平均值的系数(默认值:0.999)。

• epsilon – 添加到分母以提高数值稳定性的常数(默认值:1e-8)。

Returns:

一个 Adamax 优化器。

Example:

import numpy as np
from pyvqnet.optim import adamax
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = adamax.Adamax(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0., 0.9900000, 1.9900000, 2.9900000],
#  [3.9900000, 4.9899998, 5.9899998, 6.9899998],
#  [7.9899998, 8.9899998, 9.9899998, 10.9899998]],
# [[11.9899998, 12.9899998, 13.9899998, 14.9899998],
#  [15.9899998, 16.9899998, 17.9899998, 18.9899998],
#  [19.9899998, 20.9899998, 21.9899998, 22.9899998]]]
# ]

# [
# [[[0., 0.9800000, 1.9800000, 2.9800000],
#  [3.9800000, 4.9799995, 5.9799995, 6.9799995],
#  [7.9799995, 8.9799995, 9.9799995, 10.9799995]],
# [[11.9799995, 12.9799995, 13.9799995, 14.9799995],
#  [15.9799995, 16.9799995, 17.9799995, 18.9799995],
#  [19.9799995, 20.9799995, 21.9799995, 22.9799995]]]
# ]

RMSProp

class pyvqnet.optim.rmsprop.RMSProp(params, lr=0.01, beta=0.99, epsilon=1e-08)

RMSprop 均方根传播算法优化器。

参考:https://arxiv.org/pdf/1308.0850v5.pdf。

\[s_{t+1} = s_{t} + (1 - \beta)*(g)^2\]

\[param_new = param - \frac{g}{\sqrt{s_{t+1}} + epsilon}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• beta – 用于计算梯度及其平方的运行平均值的系数(默认值:0.99)。

• epsilon – 添加到分母以提高数值稳定性的常数(默认值:1e-8)。

Returns:

一个 RMSProp 优化器。

Example:

import numpy as np
from pyvqnet.optim import rmsprop
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = rmsprop.RMSProp(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0., 0.9000000, 1.9000000, 2.8999999],
#  [3.8999999, 4.9000001, 5.9000001, 6.9000001],
#  [7.9000001, 8.8999996, 9.8999996, 10.8999996]],
# [[11.8999996, 12.8999996, 13.8999996, 14.8999996],
#  [15.8999996, 16.8999996, 17.8999996, 18.8999996],
#  [19.8999996, 20.8999996, 21.8999996, 22.8999996]]]
# ]

# [
# [[[0., 0.8291118, 1.8291118, 2.8291118],
#  [3.8291118, 4.8291121, 5.8291121, 6.8291121],
#  [7.8291121, 8.8291111, 9.8291111, 10.8291111]],
# [[11.8291111, 12.8291111, 13.8291111, 14.8291111],
#  [15.8291111, 16.8291111, 17.8291111, 18.8291111],
#  [19.8291111, 20.8291111, 21.8291111, 22.8291111]]]
# ]

SGD

class pyvqnet.optim.sgd.SGD(params, lr=0.01, momentum=0, nesterov=False)

随机梯度下降优化器。

参考:https://en.wikipedia.org/wiki/Stochastic_gradient_descent。

\[\begin{split}\\param\_new=param-lr*g\\\end{split}\]

Parameters:

• params – 需要优化的模型参数。

• lr – 学习率(默认值:0.01)。

• momentum – 动量因子(默认值:0)。

• nesterov – 启用 Nesterov 动量 (默认: False)。

Returns:

一个 SGD 优化器。

Example:

import numpy as np
from pyvqnet.optim import sgd
from pyvqnet.tensor import QTensor
w = np.arange(24).reshape(1,2,3,4).astype(np.float64)
param = QTensor(w)
param.grad = QTensor(np.arange(24).reshape(1,2,3,4).astype(np.float64))
params = [param]
opti = sgd.SGD(params)

for i in range(1,3):
    opti._step()
    print(param)

# [
# [[[0., 0.9900000, 1.9800000, 2.9700000],
#  [3.9600000, 4.9499998, 5.9400001, 6.9299998],
#  [7.9200001, 8.9099998, 9.8999996, 10.8900003]],
# [[11.8800001, 12.8699999, 13.8599997, 14.8500004],
#  [15.8400002, 16.8299999, 17.8199997, 18.8099995],
#  [19.7999992, 20.7900009, 21.7800007, 22.7700005]]]
# ]

# [
# [[[0., 0.9800000, 1.9600000, 2.9400001],
#  [3.9200001, 4.8999996, 5.8800001, 6.8599997],
#  [7.8400002, 8.8199997, 9.7999992, 10.7800007]],
# [[11.7600002, 12.7399998, 13.7199993, 14.7000008],
#  [15.6800003, 16.6599998, 17.6399994, 18.6199989],
#  [19.5999985, 20.5800018, 21.5600014, 22.5400009]]]
# ]

Rotosolve

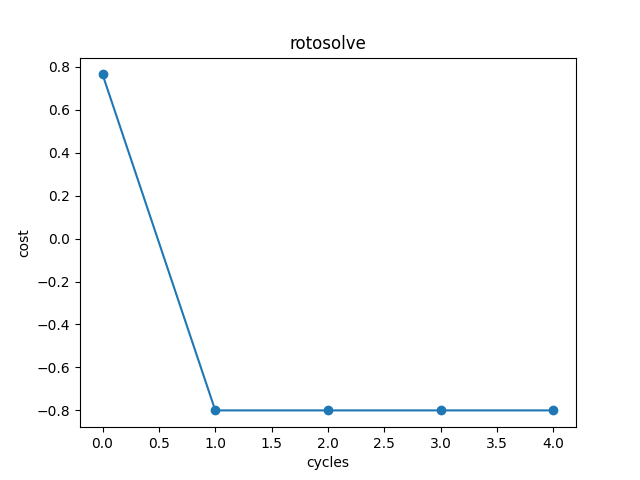
Rotosolve算法它允许相对于其他参数的固定值直接跳转到单个参数的最佳值,直接找到量子线路最佳参数的优化算法。

class pyvqnet.optim.rotosolve.Rotosolve(max_iter=50)

Rotosolve:可以使用 rotosolve 算法来最小化线性组合的量子测量期望值。 请参阅以下论文:

https://arxiv.org/abs/1903.12166, Ken M. Nakanishi。

https://arxiv.org/abs/1905.09692, Mateusz Ostaszewski。

Parameters:

max_iter – rotosolve 更新的最大迭代次数。

Returns:

一个 Rotosolve 优化器。

Example:

from pyvqnet.optim.rotosolve import Rotosolve
import pyqpanda as pq
from pyvqnet.tensor import QTensor,kfloat64
from pyvqnet.qnn.measure import expval
machine = pq.CPUQVM()
machine.init_qvm()
nqbits = machine.qAlloc_many(2)


def gen(param, generators, qbits, circuit):
    if generators == "X":
        circuit.insert(pq.RX(qbits, param))
    elif generators == "Y":
        circuit.insert(pq.RY(qbits, param))
    else:
        circuit.insert(pq.RZ(qbits, param))


def circuits(params, generators, circuit):
    gen(params[0], generators[0], nqbits[0], circuit)
    gen(params[1], generators[1], nqbits[1], circuit)
    circuit.insert(pq.CNOT(nqbits[0], nqbits[1]))
    prog = pq.QProg()
    prog.insert(circuit)
    return prog


def ansatz1(params: QTensor, generators):
    circuit = pq.QCircuit()
    params = params.getdata()
    prog = circuits(params, generators, circuit)
    return expval(machine, prog, {"Z0": 1},
                nqbits), expval(machine, prog, {"Y1": 1}, nqbits)


def ansatz2(params: QTensor, generators):
    circuit = pq.QCircuit()
    params = params.getdata()
    prog = circuits(params, generators, circuit)
    return expval(machine, prog, {"X0": 1}, nqbits)


def loss(params):
    Z, Y = ansatz1(params, ["X", "Y"])
    X = ansatz2(params, ["X", "Y"])
    return 0.5 * Y + 0.8 * Z - 0.2 * X


t = QTensor([0.3, 0.25],dtype=kfloat64)
opt = Rotosolve(max_iter=5)

costs_rotosolve = opt.minimize(t, loss)
print(costs_rotosolve)
#[0.7642691884821847, -0.799999999999997, -0.799999999999997, -0.799999999999997, -0.799999999999997]

指标模块

MSE

class pyvqnet.utils.metrics.MSE(y_true_Qtensor, y_pred_Qtensor)

计算均方误差 (Mean Squared Error, MSE)。

Parameters:

• y_true_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，真实目标值。

• y_pred_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，估计目标值。

Returns:

输出float结果。

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.MSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 9.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.MSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 9.0

RMSE

class pyvqnet.utils.metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)

计算均方根误差 (Root Mean Square Error, RMSE) 。

Parameters:

• y_true_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，真实目标值。

• y_pred_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，估计目标值。

Returns:

输出float结果。

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.RMSE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

MAE

class pyvqnet.utils.metrics.MAE(y_true_Qtensor, y_pred_Qtensor)

计算预测值和真实值之间绝对平均误差 (Mean Absolute Error , MAE) 。

Parameters:

• y_true_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入,真实目标值。

• y_pred_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入,估计目标值。

Returns:

输出float结果。

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.MAE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.MAE(y_true_Qtensor, y_pred_Qtensor)
print(result)
# 3.0

R_Square

class pyvqnet.utils.metrics.R_Square(y_true_Qtensor, y_pred_Qtensor, sample_weight=None)

计算预测值和真实值之间的R方分数。 可能的最佳分数为1.0，可以为负(因为模型可以任意恶化)。不考虑输入特征的常数模型，将获得0.0的R^2分数。

Parameters:

• y_true_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，真实目标值。

• y_pred_Qtensor – 形状类似(n_samples,)或(n_samples, n_outputs)的输入，估计目标值。

• sample_weight – 形状类似(n_samples,)的数组，可选样本权重，默认为None。

Returns:

输出float结果。

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.arange(1, 12)
y_pred_Qtensor = tensor.arange(4, 15)
result = vqnet_metrics.R_Square(y_true_Qtensor, y_pred_Qtensor)
print(result) # 0.09999999999999998

y_true_Qtensor = tensor.arange(1, 13).reshape([3, 4])
y_pred_Qtensor = tensor.arange(4, 16).reshape([3, 4])
result = vqnet_metrics.R_Square(y_true_Qtensor, y_pred_Qtensor)
print(result) # 0.15625

precision_recall_f1_2_score

class pyvqnet.utils.metrics.precision_recall_f1_2_score(y_true_Qtensor, y_pred_Qtensor)

计算2分类任务下预测值的精确率，召回率和F1分数。其中预测值和真值需要是形状类似(n_samples,)的QTensor，值为0或1，代表两个类的标签。

Parameters:

• y_true_Qtensor – 一维QTensor的输入，形状类似(n_samples,)，真实目标值。

• y_pred_Qtensor – 一维QTensor的输入，形状类似(n_samples,)，估计目标值。

Returns:

• precision - 精确率

• recall - 召回率

• f1 - F1 分数

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y_true_Qtensor = tensor.QTensor([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
y_pred_Qtensor = tensor.QTensor([0, 0, 1, 1, 1, 0, 0, 1, 1, 1])

precision, recall, f1 = vqnet_metrics.precision_recall_f1_2_score(
    y_true_Qtensor, y_pred_Qtensor)
print(precision, recall, f1)
# 0.5 0.6 0.5454545454545454

precision_recall_f1_N_score

class pyvqnet.utils.metrics.precision_recall_f1_N_score(y_true_Qtensor, y_pred_Qtensor, N, average)

多分类任务的精确率，召回率，F1分数计算。其中预测值和真值是形状类似(n_samples,)的QTensor，值为0到N-1的整数，代表N个类的标签。

Parameters:

• y_true_Qtensor – 一维QTensor的输入，真实目标值。

• y_pred_Qtensor – 一维QTensor的输入，估计目标值。

• N – N类(类别数)。

• average –

  string, [‘micro’, ‘macro’, ‘weighted’]。 多类/多标签目标需要此参数。 'micro': 通过计算总真正数来全局计算指标，假阴性和假阳性。

  'macro': 计算每个标签的指标，并找到其未加权值。意思是不考虑标签的平衡。

  'weighted': 计算每个标签的指标，并找到它们的平均值(每个标签的真实实例数)。这改变 'macro' 以解释标签不平衡; 这可能会导致F分数不在精度和召回之间。

Returns:

• precision - 精确率

• recall - 召回率

• f1 - F1 分数

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

reference_list = [1, 1, 2, 2, 2, 3, 3, 3, 3, 3]
prediciton_list = [1, 2, 2, 2, 3, 1, 2, 3, 3, 3]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

precision_micro, recall_micro, f1_micro = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='micro')
print(precision_micro, recall_micro, f1_micro)
# 0.6 0.6 0.6

precision_macro, recall_macro, f1_macro = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='macro')
print(precision_macro, recall_macro, f1_macro)
# 0.5833333333333334 0.5888888888888889 0.5793650793650794

precision_weighted, recall_weighted, f1_weighted = vqnet_metrics.precision_recall_f1_N_score(
    y_true_Qtensor, y_pred_Qtensor, 3, average='weighted')
print(precision_weighted, recall_weighted, f1_weighted)
# 0.625 0.6 0.6047619047619047

precision_recall_f1_Multi_score

class pyvqnet.utils.metrics.precision_recall_f1_Multi_score(y_true_Qtensor, y_pred_Qtensor, N, average)

多分类任务的精确率，召回率，F1分数计算。其中预测值和真值是形状类似(n_samples,N)的QTensor，预测值和真实标签必须为0-1独热编码的形式。

Parameters:

• y_true_Qtensor – 二维QTensor的输入，真实目标值。

• y_pred_Qtensor – 二维QTensor的输入，估计目标值。

• N – N类(类别数)。

• average –

  string, [‘micro’, ‘macro’, ‘weighted’]。 多类/多标签目标需要此参数。 'micro': 通过计算总真正数来全局计算指标，假阴性和假阳性。

  'macro': 计算每个标签的指标，并找到其未加权值。意思是不考虑标签的平衡。

  'weighted': 计算每个标签的指标，并找到它们的平均值(每个标签的真实实例数)。这改变 'macro' 以解释标签不平衡; 这可能会导致F分数不在精度和召回之间。

Returns:

• precision - 精确率

• recall - 召回率

• f1 - F1 分数

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

reference_list = [[1, 0], [0, 1], [0, 0], [1, 1], [1, 0]]
prediciton_list = [[1, 0], [0, 0], [1, 0], [0, 0], [0, 0]]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

micro_precision, micro_recall, micro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='micro')
print(micro_precision, micro_recall, micro_f1) # 0.5 0.2 0.28571428571428575

macro_precision, macro_recall, macro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='macro')
print(macro_precision, macro_recall, macro_f1) # 0.25 0.16666666666666666 0.2

weighted_precision, weighted_recall, weighted_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 2, average='weighted')
print(weighted_precision, weighted_recall, weighted_f1) # 0.3 0.19999999999999998 0.24

reference_list = [[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 1, 0], [1, 0, 1]]
prediciton_list = [[1, 0, 0], [1, 0, 0], [1, 1, 1], [1, 0, 0], [0, 1, 1]]
y_true_Qtensor = tensor.QTensor(reference_list)
y_pred_Qtensor = tensor.QTensor(prediciton_list)

micro_precision, micro_recall, micro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='micro')
print(micro_precision, micro_recall, micro_f1) # 0.5 0.5714285714285714 0.5333333333333333

macro_precision, macro_recall, macro_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='macro')
print(macro_precision, macro_recall, macro_f1) # 0.5 0.5555555555555555 0.5238095238095238

weighted_precision, weighted_recall, weighted_f1 = vqnet_metrics.precision_recall_f1_Multi_score(y_true_Qtensor,
            y_pred_Qtensor, 3, average='weighted')
print(weighted_precision, weighted_recall, weighted_f1) # 0.5 0.5714285714285714 0.5306122448979592

auc_calculate

class pyvqnet.utils.metrics.auc_calculate(y_true_Qtensor, y_pred_Qtensor, pos_label=None, sample_weight=None, drop_intermediate=True)

计算模型对预测值和真值之间进行分类获取的(Area Under Curve, AUC)结果。

Parameters:

• y_true_Qtensor – 一维QTensor的输入,shape = [n_samples]。 真正的二进制标签。如果标签不是{1,1}或{0,1}，则pos_label应明确给出。

• y_pred_Qtensor – 一维QTensor的输入,shape = [n_samples]。 目标分数,可以是正的概率估计类别、置信值或决策的非阈值度量(由某些分类器上的“决策函数”返回)

• pos_label – int 或 str,正类的标签。默认为None。 当 pos_label 是 None 时，如果 y_true_Qtensor 位于{-1,1}或{0,1}， pos_label 设置为1，否则将引发错误。

• sample_weight – 形状(n_samples,)的数组，默认为None。

• drop_intermediate – boolean，是否降低一些在绘制的ROC曲线上不会出现的次优阈值。(默认为None)。

Returns:

输出float结果。

Example:

import numpy as np
from pyvqnet.tensor import tensor
from pyvqnet.utils import metrics as vqnet_metrics
from pyvqnet import _core
_vqnet = _core.vqnet

y = np.array([1, 1, 1, 1, 0, 1, 0, 0, 0, 0])
pred = np.array([0.9, 0.8, 0.7, 0.6, 0.6, 0.4, 0.4, 0.3, 0.2, 0.1])
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor)
print("auc:", result) # 0.92

y = np.array([1, 1, 1, 1, 1, 0, 0, 1, 1, 1])
pred = np.array([1, 0, 1, 1, 1, 1, 0, 1, 1, 0])
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor)
print("auc:", result) # 0.625

y = [1, 2, 1, 1, 1, 0, 0, 1, 1, 1]
pred = [1, 0, 2, 1, 1, 1, 0, 1, 1, 0]
y_Qtensor = tensor.QTensor(y)
pred_Qtensor = tensor.QTensor(pred)
result = vqnet_metrics.auc_calculate(y_Qtensor, pred_Qtensor, pos_label=2)
print("auc:", result) # 0.1111111111111111

分布式计算模块

环境部署

以下介绍分别分别基于CPU、GPU分布式计算Linux系统下环境的部署.

MPI安装

MPI为CPU间通信的常用库, VQNet中CPU的分布式计算功能则基于MPI进行实现,以下将介绍如何在Linux系统中对MPI进行安装(目前基于CPU的分布式计算功能仅在Linux上实现)。

检测gcc、gfortran编译器是否安装。

which gcc
which gfortran

当显示了gcc和gfortran的路径，即可进行下一步的安装，若没有相应的编译器，请先安装编译器。当检查完编译器之后，使用wget命令下载。

wget http://www.mpich.org/static/downloads/3.3.2/mpich-3.3.2.tar.gz
tar -zxvf mpich-3.3.2.tar.gz
cd mpich-3.3.2
./configure --prefix=/usr/local/mpich
make
make install

完成mpich的编译安装，配置其环境变量

vim ~/.bashrc

# 在文档最下面加入
export PATH="/usr/local/mpich/bin:$PATH"

保存退出之后 使用source执行

source ~/.bashrc

用which来检验下配置的环境变量是否正确。显示了其路径, 则说明安装顺利完成。

此外通过pip install完成mpi4py的安装即可, 若是出现以下类似错误

为mpi4py与python版本之间不兼容的问题, 可以通过以下方法解决

# 通过下列代码暂存当前python环境的编译器
pushd /root/anaconda3/envs/mpi39/compiler_compat && mv ld ld.bak && popd

# 再次安装
pip install mpi4py

# 还原
pushd /root/anaconda3/envs/mpi39/compiler_compat && mv ld.bak ld && popd

NCCL安装

NCCL为GPU间通信的常用库, VQNet中GPU的分布式计算功能则基于NCCL进行实现,以下介绍如何在Linux系统中对NCCL进行安装(目前基于GPU的分布式计算功能仅在Linux上实现).

该部分需要MPI的支持, 因此MPI的环境也需要进行部署。

从github上将NCCL的仓库拉到本地:

git clone https://github.com/NVIDIA/nccl.git

进入nccl根目录并编译

cd nccl
make -j src.build

如果cuda没有安装到默认的路径即/usr/local/cuda, 则需要定义CUDA的路径, 使用以下代码来编译

make src.build CUDA_HOME=<path to cuda install>

并且可以根据BUILDDIR指定安装目录, 指令如下

make src.build CUDA_HOME=<path to cuda install> BUILDDIR=/usr/local/nccl

安装完成后在.bashrc文件中添加配置

vim ~/.bashrc

# 在最下面加入
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/nccl/lib
export PATH=$PATH:/usr/local/nccl/bin

保存后, 执行

source ~/.bashrc

可以通过nccl-test进行验证

git clone https://github.com/NVIDIA/nccl-tests.git
cd nccl-tests
make -j12 CUDA_HOME=/usr/local/cuda
./build/all_reduce_perf -b 8 -e 256M -f 2 -g 1

节点间通信环境部署

在多节点上实现分布式计算，首先需要保证多节点上mpich环境的一致，python环境一致，其次，需要设置节点间的免密通信。 假设需要设置node0（主节点）、node1、node2三个节点的免密通信。

# 在每个节点上执行
ssh-keygen

# 之后一直回车，在.ssh文件夹下生成一个公钥（id_rsa.pub）一个私钥（id_rsa）
# 将其另外两个节点的公钥都添加到第一个节点的authorized_keys文件中，
# 再将第一个节点authorized_keys文件传到另外两个节点便可以实现节点间的免密通信
# 在子节点node1上执行
cat ~/.ssh/id_dsa.pub >> node0:~/.ssh/authorized_keys

# 在子节点node2上执行
cat ~/.ssh/id_dsa.pub >> node0:~/.ssh/authorized_keys

# 先删除node1、node2中的authorized_keys文件后，在node0上将authorized_keys文件拷贝到另外两个节点上
scp ~/.ssh/authorized_keys  node1:~/.ssh/authorized_keys
scp ~/.ssh/authorized_keys  node2:~/.ssh/authorized_keys

# 保证三个不同节点生成的公钥都在authorized_keys文件中,即可实现节点间的免密通信

除此外，最好还设置一个共享目录，使得改变共享目录下的文件时，不同节点中文件也会进行更改，预防多节点运行模型时不同节点中的文件不同步的问题。 使用nfs-utils和rpcbind实现共享目录。

# 安装软件包
yum -y install nfs* rpcbind

# 编辑主节点上配置文件
vim /etc/exports
/data/mpi *(rw,sync,no_all_squash,no_subtree_check)

# 主节点上启动服务
systemctl start rpcbind
systemctl start nfs

# 在所有子结点node1,node2上mount要共享的目录
mount node1:/data/mpi/ /data/mpi
mount node2:/data/mpi/ /data/mpi

CPU分布式计算接口及样例

本块介绍如何在cpu硬件平台上, 利用VQNet分布式计算接口实现数据并行训练模型(目前仅支持在Linux系统上)。

init_process

使用 init_process 对分布式计算参数进行初始化。

pyvqnet.distributed.init.init_process(size, path, hostpath=None, train_size=None, test_size=None, shuffle=False)

设置分布式计算参数。

Parameters:

• size – 进程数。

• path – 当前运行文件绝对路径。

• hostpath – 多节点配置文件绝对路径。

• train_size – 训练集大小。

• test_size – 测试集大小。

• shuffle – 是否随机采样。

Example:

import argparse
import os
from pyvqnet.distributed import *

parser = argparse.ArgumentParser(description='parser example')
parser.add_argument('--init', default=False, type=bool, help='whether to use multiprocessing')
parser.add_argument('--np', default=1, type=int, help='number of processes')
parser.add_argument('--hostpath', default=None, type=str, help='multi node configuration files')
parser.add_argument('--shuffle', default=False, type=bool, help='shuffle')
parser.add_argument('--train_size', default=120, type=int, help='train_size')
parser.add_argument('--test_size', default=50, type=int, help='test_size')
args = parser.parse_args()

if(args.init):
    init_process(args.np, os.path.realpath(__file__))
else:
    break

# python run.py --init true --np 2

average_parameters_allreduce

使用 average_parameters_allreduce 以allreduce的方式对不同进程上模型参数进行传递并以平均值更新。

pyvqnet.distributed.comm.average_parameters_allreduce(model)

设置分布式计算参数。

Parameters:

model – Module - 训练的模型.

Returns:

参数更新后的模型.

Example:

from pyvqnet.distributed import average_parameters_allreduce
import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed import *

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)

    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net()
print(f"rank {get_rank()} parameters is {model.parameters()}")
model = average_parameters_allreduce(model)

if get_rank() == 0:
    print(model.parameters())

# mpirun -n 2 python run.py

average_grad_allreduce

使用 average_grad_allreduce 以allreduce的方式对不同进程上模型参数梯度进行传递并以平均值更新.

pyvqnet.distributed.comm.average_grad_allreduce(optimizer)

设置分布式计算参数。

Parameters:

optimizer – optimizer.

Returns:

梯度更新后的优化器。

Example:

from pyvqnet.distributed import average_grad_allreduce
import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed import *
from pyvqnet.nn.loss import MeanSquaredError
from pyvqnet.optim import Adam

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)

    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x
model = Net()
opti = Adam(model.parameters(), lr=0.01)
actual = tensor.QTensor([1,1,1,1,1,0,0,0,0,0],dtype=6).reshape((10,1))

x = tensor.randn((10, 5))
for i in range(10):
    opti.zero_grad()
    model.train()

    result = model(x)
    loss = MeanSquaredError()(actual, result)
    loss.backward()

    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti = average_grad_allreduce(opti)
    # if get_rank() == 0 :
    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti.step()


# mpirun -n 2 python run.py

average_parameters_reduce

使用 average_parameters_reduce 以reduce的方式对进程上模型参数进行传递, 并对指定进程上的参数进行更新。

pyvqnet.distributed.comm.average_parameters_reduce(model, root=0)

设置分布式计算参数。

Parameters:

• model – Module - 训练的模型.

• root – 指定的进程号.

Returns:

参数更新后的模型。

Example:

from pyvqnet.distributed import average_parameters_reduce
import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed import *

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)

    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x


model = Net()
print(f"rank {get_rank()} parameters is {model.parameters()}")
model = average_parameters_reduce(model)

if get_rank() == 0:
    print(model.parameters())

# mpirun -n 2 python run.py

average_grad_reduce

使用 average_grad_reduce 以reduce的方式对进程上参数的梯度进行传递， 并对指定进程上的参数梯度更新。

pyvqnet.distributed.comm.average_grad_reduce(optimizer, root=0)

设置分布式计算参数。

Parameters:

• optimizer – optimizer.

• root – 指定的进程号.

Returns:

梯度更新后的优化器.

Example:

from pyvqnet.distributed import average_grad_reduce
import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed import *
from pyvqnet.nn.loss import MeanSquaredError
from pyvqnet.optim import Adam

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)

    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x
model = Net()
opti = Adam(model.parameters(), lr=0.01)
actual = tensor.QTensor([1,1,1,1,1,0,0,0,0,0],dtype=6).reshape((10,1))

x = tensor.randn((10, 5))
for i in range(10):
    opti.zero_grad()
    model.train()

    result = model(x)
    loss = MeanSquaredError()(actual, result)
    loss.backward()

    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti = average_grad_reduce(opti)
    # if get_rank() == 0 :
    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti.step()

# mpirun -n 2 python run.py

样例

导入相关库

import sys
sys.path.insert(0,"../")
import time
import os
import struct
import gzip
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn.conv import Conv2D

from pyvqnet.nn import activation as F
from pyvqnet.nn.pooling import MaxPool2D
from pyvqnet.nn.loss import CategoricalCrossEntropy
from pyvqnet.optim.adam import Adam
from pyvqnet.data.data import data_generator
from pyvqnet.tensor import tensor
from pyvqnet.tensor.tensor import QTensor
import pyqpanda as pq
import time
import numpy as np
import matplotlib
from pyvqnet.distributed import *  # 分布式计算模块
import argparse

数据获取

url_base = "http://yann.lecun.com/exdb/mnist/"
key_file = {
    "train_img": "train-images-idx3-ubyte.gz",
    "train_label": "train-labels-idx1-ubyte.gz",
    "test_img": "t10k-images-idx3-ubyte.gz",
    "test_label": "t10k-labels-idx1-ubyte.gz"
}
if_show_sample = 0
grad_time = []
forward_time = []
forward_time_sum = []

def _download(dataset_dir, file_name):
    """
    Download mnist data if needed.
    """
    file_path = dataset_dir + "/" + file_name

    if os.path.exists(file_path):
        with gzip.GzipFile(file_path) as file:
            file_path_ungz = file_path[:-3].replace("\\", "/")
            if not os.path.exists(file_path_ungz):
                open(file_path_ungz, "wb").write(file.read())
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    if os.path.exists(file_path):
        with gzip.GzipFile(file_path) as file:
            file_path_ungz = file_path[:-3].replace("\\", "/")
            file_path_ungz = file_path_ungz.replace("-idx", ".idx")
            if not os.path.exists(file_path_ungz):
                open(file_path_ungz, "wb").write(file.read())
    print("Done")


def download_mnist(dataset_dir):
    for v in key_file.values():
        _download(dataset_dir, v)

def load_mnist(dataset="training_data", digits=np.arange(2), path="./"):
    """
    load mnist data
    """
    from array import array as pyarray
    download_mnist(path)
    if dataset == "training_data":
        fname_image = os.path.join(path, "train-images.idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "train-labels.idx1-ubyte").replace(
            "\\", "/")
    elif dataset == "testing_data":
        fname_image = os.path.join(path, "t10k-images.idx3-ubyte").replace(
            "\\", "/")
        fname_label = os.path.join(path, "t10k-labels.idx1-ubyte").replace(
            "\\", "/")
    else:
        raise ValueError("dataset must be 'training_data' or 'testing_data'")

    flbl = open(fname_label, "rb")
    _, size = struct.unpack(">II", flbl.read(8))
    lbl = pyarray("b", flbl.read())
    flbl.close()

    fimg = open(fname_image, "rb")
    _, size, rows, cols = struct.unpack(">IIII", fimg.read(16))
    img = pyarray("B", fimg.read())
    fimg.close()

    ind = [k for k in range(size) if lbl[k] in digits]
    num = len(ind)
    images = np.zeros((num, rows, cols))
    labels = np.zeros((num, 1), dtype=int)
    for i in range(len(ind)):
        images[i] = np.array(img[ind[i] * rows * cols:(ind[i] + 1) * rows *
                                 cols]).reshape((rows, cols))
        labels[i] = lbl[ind[i]]

    return images, labels


def data_select(train_num, test_num):
    """
    Select data from mnist dataset.
    """

    x_train, y_train = load_mnist("training_data")  # 下载训练数据
    x_test, y_test = load_mnist("testing_data")
    idx_train = np.append(
            np.where(y_train == 0)[0][0:train_num],
            np.where(y_train == 1)[0][0:train_num])
    x_train = x_train[idx_train]
    y_train = y_train[idx_train]
    x_train = x_train / 255
    y_train = np.eye(2)[y_train].reshape(-1, 2)

    idx_test = np.append(
            np.where(y_test == 0)[0][:test_num],
            np.where(y_test == 1)[0][:test_num])
    x_test = x_test[idx_test]
    y_test = y_test[idx_test]
    x_test = x_test / 255
    y_test = np.eye(2)[y_test].reshape(-1, 2)

    return x_train, y_train, x_test, y_test

模型定义

def circuit_func(weights):
    """
    A function using QPanda to create quantum circuits and run.
    """
    num_qubits = 1
    machine = pq.CPUQVM()
    machine.init_qvm()
    qubits = machine.qAlloc_many(num_qubits)
    cbits = machine.cAlloc_many(num_qubits)
    circuit = pq.QCircuit()
    circuit.insert(pq.H(qubits[0]))
    circuit.insert(pq.RY(qubits[0], weights[0]))
    prog = pq.QProg()
    prog.insert(circuit)
    prog << pq.measure_all(qubits, cbits)  #pylint:disable=expression-not-assigned

    result = machine.run_with_configuration(prog, cbits, 1000)

    counts = np.array(list(result.values()))
    states = np.array(list(result.keys())).astype(float)
    # Compute probabilities for each state
    probabilities = counts / 100
    # Get state expectation
    expectation = np.sum(states * probabilities)
    return expectation

class Hybrid(Module):
    """ Hybrid quantum - Quantum layer definition """
    def __init__(self, shift):
        super(Hybrid, self).__init__()
        self.shift = shift
        self.input = None

    def forward(self, x):
        self.input = x
        expectation_z = circuit_func(np.array(x.data))
        result = [[expectation_z]]
        # requires_grad = x.requires_grad and not QTensor.NO_GRAD
        requires_grad = x.requires_grad
        def _backward_mnist(g, x):
            """ Backward pass computation """
            start_grad_time = time.time()
            input_list = np.array(x.data)
            shift_right = input_list + np.ones(input_list.shape) * self.shift
            shift_left = input_list - np.ones(input_list.shape) * self.shift

            gradients = []
            for i in range(len(input_list)):
                expectation_right = circuit_func(shift_right[i])
                expectation_left = circuit_func(shift_left[i])
                gradient = expectation_right - expectation_left
                gradients.append(gradient)
            gradients = np.array([gradients]).T

            end_grad_time = time.time()
            grad_time.append(end_grad_time - start_grad_time)
            in_g = gradients * np.array(g)
            return in_g

        nodes = []
        if x.requires_grad:
            nodes.append(
                QTensor.GraphNode(tensor=x,
                                  df=lambda g: _backward_mnist(g, x)))
        return QTensor(data=result, requires_grad=requires_grad, nodes=nodes)


class Net(Module):
    """
    Hybird Quantum Classci Neural Network Module
    """
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = Conv2D(input_channels=1,
                            output_channels=6,
                            kernel_size=(5, 5),
                            stride=(1, 1),
                            padding="valid")
        self.maxpool1 = MaxPool2D([2, 2], [2, 2], padding="valid")
        self.conv2 = Conv2D(input_channels=6,
                            output_channels=16,
                            kernel_size=(5, 5),
                            stride=(1, 1),
                            padding="valid")
        self.maxpool2 = MaxPool2D([2, 2], [2, 2], padding="valid")

        self.fc1 = Linear(input_channels=256, output_channels=64)
        self.fc2 = Linear(input_channels=64, output_channels=1)

        self.hybrid = Hybrid(np.pi / 2)
        self.fc3 = Linear(input_channels=1, output_channels=2)

    def forward(self, x):
        start_time_forward = time.time()
        x = F.ReLu()(self.conv1(x))

        x = self.maxpool1(x)
        x = F.ReLu()(self.conv2(x))

        x = self.maxpool2(x)
        x = tensor.flatten(x, 1)

        x = F.ReLu()(self.fc1(x))
        x = self.fc2(x)

        start_time_hybrid = time.time()
        x = self.hybrid(x)

        end_time_hybrid = time.time()

        forward_time.append(end_time_hybrid - start_time_hybrid)

        x = self.fc3(x)
        end_time_forward = time.time()
        forward_time_sum.append(end_time_forward - start_time_forward)
        return x

在训练时引用split_data、average_parameters_allreduce、init_process实现基于CPU数据并行的分布式计算。

使用方法如下

def run(args):
    """
    Run mnist train function
    """
    x_train, y_train, x_test, y_test = data_select(args.train_size, args.test_size)

    x_train, y_train= split_data(x_train, y_train) # 分布式模块接口对数据切分
    print(get_rank())
    model = Net()
    optimizer = Adam(model.parameters(), lr=0.001)
    loss_func = CategoricalCrossEntropy()

    epochs = 10
    train_loss_list = []
    val_loss_list = []
    train_acc_list = []
    val_acc_list = []
    model.train()

    for epoch in range(1, epochs):
        total_loss = []
        model.train()
        batch_size = 1
        correct = 0
        n_train = 0

        for x, y in data_generator(x_train,
                                   y_train,
                                   batch_size=1,
                                   shuffle=False):

            x = x.reshape(-1, 1, 28, 28)

            optimizer.zero_grad()
            output = model(x)
            loss = loss_func(y, output)
            loss_np = np.array(loss.data)

            np_output = np.array(output.data, copy=False)
            mask = (np_output.argmax(1) == y.argmax(1))
            correct += np.sum(np.array(mask))
            n_train += batch_size

            loss.backward()
            # optimizer = average_grad_allreduce(optimizer) 以allreduce方式对优化器中参数梯度进行传递, 并更新
            optimizer._step()

            total_loss.append(loss_np)
        model = average_parameters_allreduce(model) # 对不同rank的模型参数以allreduce方式通信, 并对参数更新


        train_loss_list.append(np.sum(total_loss) / len(total_loss))
        train_acc_list.append(np.sum(correct) / n_train)
        print("{:.0f} loss is : {:.10f}".format(epoch, train_loss_list[-1]))

        model.eval()
        correct = 0
        n_eval = 0

        for x, y in data_generator(x_test, y_test, batch_size=1, shuffle=True):
            x = x.reshape(-1, 1, 28, 28)
            output = model(x)
            loss = loss_func(y, output)
            loss_np = np.array(loss.data)
            np_output = np.array(output.data, copy=False)
            mask = (np_output.argmax(1) == y.argmax(1))
            correct += np.sum(np.array(mask))
            n_eval += 1

            total_loss.append(loss_np)
        print(f"Eval Accuracy: {correct / n_eval}")
        val_loss_list.append(np.sum(total_loss) / len(total_loss))
        val_acc_list.append(np.sum(correct) / n_eval)

if __name__ == "__main__":

    parser = argparse.ArgumentParser(description='parser example')
    parser.add_argument('--init', default=False, type=bool, help='whether to use multiprocessing')
    parser.add_argument('--np', default=1, type=int, help='number of processes')
    parser.add_argument('--hostpath', default=None, type=str, help='hosts absolute path')
    parser.add_argument('--shuffle', default=False, type=bool, help='shuffle')
    parser.add_argument('--train_size', default=120, type=int, help='train_size')
    parser.add_argument('--test_size', default=50, type=int, help='test_size')
    args = parser.parse_args()
    # p_path = os.path.realpath (__file__)

    if(args.init):
        init_process(args.np, os.path.realpath(__file__), args.hostpath, args.train_size,args.test_size, args.shuffle)
    else:
        a = time.time()
        run(args)
        b=time.time()
        if(get_rank()==0):
            print("time: {}",format(b-a))

其中init代表是否基于分布式训练模型，np代表进程数，另外hostpath文件代码在多节点上运行模型时的配置文件的绝对路径，配置文件内容包括多节点的ip以及进程分配情况,如下

node0:1
node1:1
node2:1

在命令行输入

python test_mdis.py --init true

0
1 loss is : 0.8230862300
Eval Accuracy: 0.5
        ...
9 loss is : 0.5660219193
Eval Accuracy: 0.46
time: {} 15.132369756698608


python test_mdis.py --init true --np 2

得到结果

1
1 loss is : 0.0316730281
Eval Accuracy: 0.5
        ...
9 loss is : 0.0006756162
Eval Accuracy: 0.5

0
1 loss is : 0.0072183679
Eval Accuracy: 0.85
        ...
9 loss is : 0.0001979264
Eval Accuracy: 0.82
time: {} 9.132536888122559

以上是在单节点上多进程模型训练，可以明显看出训练时间缩短

在多节点上训练，命令如下

python3 test_mdis.py --init true --np 4 --hostpath ~/example/host.txt

0
1 loss is : 0.8609524409
Eval Accuracy: 0.5
        ...
9 loss is : 0.4251357079
Eval Accuracy: 0.5
time: {} 6.5950517654418945

3
1 loss is : 0.0034498004
Eval Accuracy: 0.5
        ...
9 loss is : 0.0001483827
Eval Accuracy: 0.5

1
1 loss is : 0.0990966797
Eval Accuracy: 0.5
        ...
9 loss is : 0.0037492002
Eval Accuracy: 0.5

2
1 loss is : 0.8468652089
Eval Accuracy: 0.5
        ...
Eval Accuracy: 0.53
9 loss is : 0.4186156909
Eval Accuracy: 0.52

GPU分布式计算接口及样例

nccl_average_parameters_allreduce

使用 nccl_average_parameters_allreduce 以allreduce的方式对不同进程上模型参数进行传递并更新。

pyvqnet.distributed.nccl_api.nccl_average_parameters_allreduce(optimizer, Ncclop: NCCL_api, c_op='avg')

设置分布式计算参数。

Parameters:

• model – Module - 训练的模型.

• Ncclop – NCCL_api.

• c_op – 计算方式.

Example:

import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed.nccl_api import *

nccl_op = NCCL_api()
nccl_op.ncclCommInitRank()

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x
model = Net().toGPU(1000 + get_rank())
print(f"rank {get_rank()} parameters is {model.parameters()}")
nccl_average_parameters_allreduce(model, nccl_op)

if get_rank() == 0:
    print(model.parameters())

# mpirun -n 2 python test.py

# rank 1 parameters is [[[ 0.8647987],
#  [ 0.8910748],
#  [-0.3896213],
#  [-0.871486 ],
#  [-0.8997867]], [0.4014191]]
# rank 0 parameters is [[[-0.6880538],
#  [ 0.0963508],
#  [-0.3776291],
#  [ 0.1773794],
#  [ 0.6670241]], [-0.1019871]]
# [[[ 0.0883724],
#  [ 0.4937128],
#  [-0.3836252],
#  [-0.3470533],
#  [-0.1163813]], [0.149716]]

nccl_average_parameters_reduce

使用 nccl_average_parameters_reduce 以reduce的方式对不同进程上模型参数进行传递并更新。

pyvqnet.distributed.nccl_api.nccl_average_parameters_reduce(model, Ncclop: NCCL_api, root=0, c_op='avg')

设置分布式计算参数。

Param:

model: Module - 训练的模型.

Parameters:

• Ncclop – NCCL_api.

• root – 指定进程号.

• c_op – 计算方式.

Example:

import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed.nccl_api import *

nccl_op = NCCL_api()
nccl_op.ncclCommInitRank()

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x
model = Net().toGPU(1000 + get_rank())
print(f"rank {get_rank()} parameters is {model.parameters()}")

nccl_average_parameters_reduce(model, nccl_op)

if get_rank() == 0:
    print(model.parameters())

# mpirun -n 2 python test.py

# rank 1 parameters is [[[-0.7666817],
#  [ 0.3023796],
#  [-0.6021696],
#  [ 0.5293468],
#  [-0.1318247]], [0.4162451]]
# rank 0 parameters is [[[ 0.1145883],
#  [-0.3539237],
#  [ 0.8672745],
#  [ 0.5483069],
#  [-0.5038487]], [0.4179307]]
# [[[-0.3260467],
#  [-0.025772 ],
#  [ 0.1325525],
#  [ 0.5388269],
#  [-0.3178367]], [0.4170879]]

nccl_average_grad_allreduce

使用 nccl_average_grad_allreduce 以allreduce的方式对不同进程上参数梯度进行传递并更新。

pyvqnet.distributed.nccl_api.nccl_average_grad_allreduce(optimizer, Ncclop: NCCL_api, c_op='avg')

设置分布式计算参数。

Parameters:

• optimizer – Optimizer.

• Ncclop – NCCL_api.

• root – 指定的进程号.

Example:

import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed.nccl_api import *
from pyvqnet.nn.loss import MeanSquaredError
from pyvqnet.optim import Adam
from pyvqnet.tensor import tensor

nccl_op = NCCL_api()
nccl_op.ncclCommInitRank()

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net().toGPU(1000+ get_rank())
opti = Adam(model.parameters(), lr=0.01)

actual = tensor.QTensor([1,1,1,1,1,0,0,0,0,0],dtype=6).reshape((10,1)).toGPU(1000+get_rank())

x = tensor.randn((10, 5)).toGPU(1000+get_rank())

for i in range(10):
    opti.zero_grad()
    model.train()

    result = model(x)
    loss = MeanSquaredError()(actual, result)
    loss.backward()

    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")

    nccl_average_grad_allreduce(opti, nccl_op)
    if get_rank() == 0 :
        print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti.step()

    exit()

# mpirun -n 2 python test.py
# rank 1 grad is [[-0.2537998],
#  [-0.0411504],
#  [-0.3565139],
#  [ 0.5702319],
#  [ 0.0177623]]
# rank 0 grad is [[-0.1322807],
#  [ 0.481559 ],
#  [-0.8823745],
#  [ 0.211081 ],
#  [-0.0234532]]
# rank 0 grad is [[-0.1930403],
#  [ 0.2202043],
#  [-0.6194442],
#  [ 0.3906564],
#  [-0.0028455]]

nccl_average_grad_reduce

使用 nccl_average_grad_reduce 以reduce的方式对不同进程上参数梯度进行传递并更新。

pyvqnet.distributed.nccl_api.nccl_average_grad_reduce(optimizer, Ncclop: NCCL_api, root=0, c_op='avg')

设置分布式计算参数。

Parameters:

• optimizer – Optimizer.

• Ncclop – NCCL_api.

• root – 在指定的节点上更新参数梯度.

• c_op – 计算方式.

Example:

import numpy as np
from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed.nccl_api import *
from pyvqnet.nn.loss import MeanSquaredError
from pyvqnet.optim import Adam
from pyvqnet.tensor import tensor

nccl_op = NCCL_api()
nccl_op.ncclCommInitRank()

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net().toGPU(1000+ get_rank())
opti = Adam(model.parameters(), lr=0.01)

actual = tensor.QTensor([1,1,1,1,1,0,0,0,0,0],dtype=6).reshape((10,1)).toGPU(1000+get_rank())

x = tensor.randn((10, 5)).toGPU(1000+get_rank())

for i in range(10):
    opti.zero_grad()
    model.train()

    result = model(x)
    loss = MeanSquaredError()(actual, result)
    loss.backward()

    print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")

    nccl_average_grad_reduce(opti, nccl_op)
    if get_rank() == 0 :
        print(f"rank {get_rank()} grad is {model.parameters()[0].grad}")
    opti.step()

    exit()

# mpirun -n 2 python test.py

# rank 1 grad is [[ 0.2536973],
#  [ 0.1971456],
#  [ 0.2229966],
#  [-0.1126524],
#  [-0.4308025]]
# rank 0 grad is [[-0.7967089],
#  [ 0.3266841],
#  [ 0.087491 ],
#  [-2.0684564],
#  [ 1.0999191]]
# rank 0 grad is [[-0.2715058],
#  [ 0.2619148],
#  [ 0.1552438],
#  [-1.0905544],
#  [ 0.3345583]]

案例

from pyvqnet.qnn.vqc import *
from pyvqnet.optim import Adam
from pyvqnet.nn import Module, BinaryCrossEntropy, Sigmoid
from pyvqnet.data import data_generator
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from pyvqnet.tensor import QTensor

from pyvqnet.distributed.nccl_api import *
from pyvqnet.distributed import split_data, broadcast_model_params

from time import time


# NCCL 初始化
nccl_op = NCCL_api()
nccl_op.ncclCommInitRank()

iris_dataset = datasets.load_iris()

X1 = iris_dataset.data[:100, :].astype(
    np.float32)  # 选取iris_dataset的data的前100个数据，将其数据类型转换为float32，并储存在X中
X_feature_names = iris_dataset.feature_names  # 将iris_dataset的特征名称储存在X_feature_names中
y = iris_dataset.target[:100].astype(
    int)  # 选取iris_dataset的target的前100个数据，将其数据类型转换为int，并储存在y中
y_target_names = iris_dataset.target_names[:
                                           2]  # 选取iris_dataset的target_names的前2个数据，并储存在y_target_names中

alpha = X1[:, :
           3] * X1[:,
                   1:]  # 每一个样本中，利用相邻两个特征值计算出一个参数，即每一个样本会多出3个参数（因为有4个特征值），并储存在alpha中
X1 = np.append(X1, alpha, axis=1)  # 在axis=1的维度上，将alpha的数据值添加到X的特征值中
print(X1.shape)
# exit()
X_train, X_test, y_train, y_test = train_test_split(X1,
                                                    y,
                                                    test_size=0.2,
                                                    random_state=0,
                                                    shuffle=True)

class Q_model(Module):
    def __init__(self):
        super(Q_model, self).__init__()

        self.hardward = VQC_HardwareEfficientAnsatz(
            n_qubits=4,
            single_rot_gate_list=["ry"],
            entangle_gate="cnot",
            depth=15)
        obs_list = [{
            'wires': [2, 3],
            'observables': ['Z', 'Z'],
            'coefficient': [1, 1]
        }]
        # print(obs_list)
        self.ma = MeasureAll(obs=obs_list)
        self.ac = Sigmoid()
        self.qm = QMachine(4)

    def forward(self, input):
        qm = self.qm
        qm.reset_states(input.shape[0])

        def cir(qm, x):
            for i in range(4):
                hadamard(qm, i)

            for i in range(4):
                rz(qm, i, x[:, [i]])

            for i in range(3):
                cnot(qm, [i, i + 1])
                rz(qm, i + 1, x[:, [4 + i]])
            return qm

        qm = cir(qm, input)
        self.hardward(q_machine=qm)
        y = self.ma(q_machine=qm)
        y = self.ac(y)

        return y

def run():
    """
    Main run function
    """

    model = Q_model()
    model = broadcast_model_params(model)
    model = model.toGPU(1000 + get_rank())
    # print(model.parameters())
    optimizer = Adam(model.parameters(), lr=0.1)
    batch_size = 20
    epoch = 20
    loss = BinaryCrossEntropy()
    print("start training..............")
    model.train()

    datas, labels= split_data(X_train, y_train)

    def get_accuary(result, label):
        result = (result > 0.5).astype(4)
        score = tensor.sums(result == label)
        return score

    time2 = time()
    runtime = 0
    for i in range(epoch):
        count = 0
        sum_loss = 0
        accuary = 0
        t = 0
        for data, label in data_generator(datas, labels, batch_size, False):
            time3 = time()
            optimizer.zero_grad()
            data, label = QTensor(data,requires_grad=True).toGPU(1000 + get_rank()), QTensor(label,
                                                 dtype=6,
                                                 requires_grad=False).toGPU(1000 + get_rank())

            result = model(data)

            loss_b = loss(label.reshape([-1, 1]), result)

            loss_b.backward()

            nccl_average_grad_allreduce(optimizer, nccl_op)
            optimizer._step()

            sum_loss += loss_b.item()
            count += batch_size
            accuary += get_accuary(result, label.reshape([-1,1]))
            t = t + 1
            runtime += time() - time3

        # nccl_average_parameters_reduce(model, nccl_op)
        if get_rank()==0:
            print(
                f"epoch:{i}, #### loss:{sum_loss/count} #####accuray:{accuary/count}"
            )

    print("start testing..............")
    model.eval()
    count = 0
    if get_rank() == 0:
        print(time() - time2)
    test_data, test_label = X_test, y_test
    test_batch_size = 5
    accuary = 0
    sum_loss = 0
    for testd, testl in data_generator(test_data, test_label, test_batch_size):
        testd = QTensor(testd).toGPU(1000+get_rank())
        testl = QTensor(testl, dtype=6).toGPU(1000+get_rank())
        test_result = model(testd)
        test_loss = loss(testl.reshape([-1, 1]), test_result)
        sum_loss += test_loss
        count += test_batch_size
        accuary += get_accuary(test_result, testl.reshape([-1, 1]))
    if get_rank()==0:
        print(
            f"test:--------------->loss:{sum_loss/count} #####accuray:{accuary/count}"
        )
run()

split_data

在多进程中，使用 split_data 根据进程数对数据进行切分，返回相应进程上数据。

pyvqnet.distributed.datasplit.split_data(x_train, y_train, shuffle=False)

设置分布式计算参数。

Parameters:

• x_train – np.array - 训练数据.

• y_train – np.array - 训练数据标签.

• shuffle – bool - 是否打乱后再进行切分，默认值是False.

Returns:

切分后的训练数据和标签。

Example:

from pyvqnet.distributed import split_data
import numpy as np

x_train = np.random.randint(255, size = (100, 5))
y_train = np.random.randint(2, size = (100, 1))

x_train, y_train= split_data(x_train, y_train)

broadcast_model_params

使用 broadcast_model_params 在模型训练前将指定进程上的模型参数广播到其他进程，使模型训练前的参数保持一致。

pyvqnet.distributed.comm.broadcast_model_params(model, root=0)

设置分布式计算参数。

Parameters:

• model – Module - 训练的模型.

• root – 指定的进程号.

Example:

from pyvqnet.nn.module import Module
from pyvqnet.nn.linear import Linear
from pyvqnet.nn import activation as F
from pyvqnet.distributed import broadcast_model_params, get_rank

class Net(Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc = Linear(input_channels=5, output_channels=1)
    def forward(self, x):
        x = F.ReLu()(self.fc(x))
        return x

model = Net()
print(f"bcast before rank {get_rank()}:{model.parameters()}")
model = broadcast_model_params(model)
model = model.toGPU(1000+ get_rank())
print(f"bcast after rank {get_rank()}: {model.parameters()}")

# mpirun -n 2 python run.py